Question

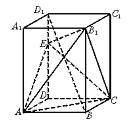
如图，已知正四棱柱ABCD—A₁B₁C₁D₁，点E在棱D₁D上，截面EAC∥D₁B，且面EAC与底面ABCD所成的角为45°，AB＝a.

（Ⅰ）求截面EAC的面积；

（Ⅱ）求异面直线A₁B₁与AC之间的距离；

（Ⅲ）求三棱锥B₁－EAC的体积.

Answer 1

答案：
解析：

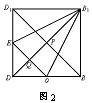
解：（Ⅰ）如图1，连结DB交AC于O，连结EO. ∵底面ABCD是正方形， ∴DO⊥AC  又∵ED⊥底面AC，  ∴EO⊥AC ∴∠EOD是面EAC与底面AC所成二面角的平面角， ∴∠EOD＝45° DO＝a，AC＝a，EO＝a·sec45°＝a， 故S△EAC=EO·AC＝a2． （Ⅱ）由题设ABCD—A1B1C1D1是正四棱柱，得A1A⊥底面AC，A1A⊥AC． 又A1A⊥A1B1，  ∴A1A是异面直线A1B1与AC间的公垂线. ∵D1B∥面EAC，且面D1BD与面EAC交线为EO， ∴D1B∥EO， 又O是DB的中点 ∴E是D1D的中点，D1B＝2EO＝2a. ∴D1D＝a 异面直线A1B1与AC间的距离为a. （Ⅲ）解法一：如图2，连结D1B1． ∵D1D＝DB＝a，  ∴BDD1B1是正方形. 连结B1D交D1B于P，交EO于Q. ∵B1D⊥D1B，EO∥D1B， ∴B1D⊥EO． 又AC⊥EO，AC⊥ED． ∴AC⊥面BDD1B1， ∴B1D⊥AC，∴B1D⊥面EAC． ∴B1Q是三棱锥B1—EAC的高. 由DQ＝PQ，得B11＝B1D＝a ∴． 所以三棱锥B1—EAC的体积是a3. 解法二：连结B1O，则 ∵AO⊥面BDD1B1， ∴AO是三棱锥A—EOB1的高，AO＝a. 在正方形BDD1B1中，E、O分别是D1D、DB的中点，则 . ∴. 所以三棱锥B1—EAC的体积是a3．