题目内容
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.(1)求截面EAC的面积;
(2)求异面直线A1B1与AC之间的距离;
(3)求三棱锥B1-BAC的体积.
分析:(1)如图,利用∠EOD是面EAC与底面AC所成二面角的平面角,结合直角三角形中的边角关系即可求得截面EAC的面积;
(2)先证明A1A是异面直线A1B1与AC间的公垂线,再利用直角三角形中勾股定理即可求得线段A1A的长度;
(3)欲求三棱锥B1-BAC的体积,考虑到则VB1-EAC=2VA-EOB1先求三棱锥A-EOB1的体积即可.
(2)先证明A1A是异面直线A1B1与AC间的公垂线,再利用直角三角形中勾股定理即可求得线段A1A的长度;
(3)欲求三棱锥B1-BAC的体积,考虑到则VB1-EAC=2VA-EOB1先求三棱锥A-EOB1的体积即可.
解答:(1)解:连接BD交AC于O,连接EO
∵底面ABCD是正方形,∴DO⊥AC
又∵ED⊥底面AC,∴EO⊥AC
∴∠EOD是面EAC与底面AC所成二面角的平面角.∴∠EOD=45°.DO=
a,AC=
a,EO=
a•sec45°=a.
故S△EAC=
a2.
(2)解:由题设ABCD-A1B1C1D1是正四棱柱,得A1A⊥底面AC,A1A⊥AC,
又A1A⊥A1B1,
∴A1A是异面直线A1B1与AC间的公垂线.∵D1B1∥面EAC,且面D1BD与面EAC交线为EO,
∴D1B1∥EO
又O是DE的中点,∴E是D1D的中点,D1B1=2EO=2a
∴D1D=
=
a.异面直线A1B1与AC间的距离为
a.
(3)解:连接B1O,则VB1-EAC=2VA-EOB1
∵AO⊥面BDD1B1,
∴AO是三棱锥A-EOB1的高,AO=
a.
在正方形BDD1B1中,E、O分别是D1D、DB的中点(如右图),则S△EOB1=
a2.
∴VB1-EAC=2•
•
a2•
a=
a3.所以三棱锥B1-EAC的体积是
a3.
∵底面ABCD是正方形,∴DO⊥AC
又∵ED⊥底面AC,∴EO⊥AC
∴∠EOD是面EAC与底面AC所成二面角的平面角.∴∠EOD=45°.DO=
| ||
| 2 |
| 2 |
| ||
| 2 |
故S△EAC=
| ||
| 2 |
(2)解:由题设ABCD-A1B1C1D1是正四棱柱,得A1A⊥底面AC,A1A⊥AC,
又A1A⊥A1B1,
∴A1A是异面直线A1B1与AC间的公垂线.∵D1B1∥面EAC,且面D1BD与面EAC交线为EO,
∴D1B1∥EO
又O是DE的中点,∴E是D1D的中点,D1B1=2EO=2a
∴D1D=
| D1B2-DB2 |
| 2 |
| 2 |
(3)解:连接B1O,则VB1-EAC=2VA-EOB1
∵AO⊥面BDD1B1,
∴AO是三棱锥A-EOB1的高,AO=
| ||
| 2 |
在正方形BDD1B1中,E、O分别是D1D、DB的中点(如右图),则S△EOB1=
| 3 |
| 4 |
∴VB1-EAC=2•
| 1 |
| 3 |
| 3 |
| 4 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
点评:本小题主要考查空间线面关系、二面角和距离的概念,逻辑思维能力、空间想象能力及运算能力.

练习册系列答案
相关题目
 如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.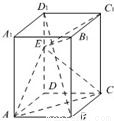 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.