题目内容
已知圆C经过两点P（-2，4），Q（3，-1），且在x轴上截得的弦长为6，求圆C的方程．
【答案】分析：设出圆C方程为：（x-a）2+（y-b）2=R2，将P与Q坐标代入得到两个关系式，再根据圆C在x轴上截得的弦长为6列出关系式，三关系式联立求出a，b及R的值，即可确定出圆C的方程．
解答：解：设圆C：（x-a）2+（y-b）2=R2，
根据题意得：
，
解得：
或
，
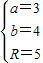∴圆C的方程为（x-1）2+（y-2）2=13或（x-3）2+（y-4）2=25．
点评：此题考查了直线与圆相交的性质，涉及的知识有：圆的标准方程，两点间的距离公式，弄清题意是解本题的关键．
解答：解：设圆C：（x-a）2+（y-b）2=R2，
根据题意得：
，解得：
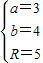或，∴圆C的方程为（x-1）2+（y-2）2=13或（x-3）2+（y-4）2=25．
点评：此题考查了直线与圆相交的性质，涉及的知识有：圆的标准方程，两点间的距离公式，弄清题意是解本题的关键．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
（2012•江苏）A．[选修4-1：几何证明选讲]