Question

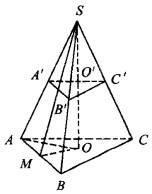
已知正三棱锥S-ABC的高SO=h，斜高SM=l，求经过SO的中点O′平行于底面的截面△A′B′C′的面积(如图所示)．

v

Answer 1

答案：
解析：

连结OM、OA，在Rt△SOM中 　　OM= 　　因为棱锥S-ABC是正棱锥，所以点O是正三角形ABC的中心 　　AB=2AM=2OM·tan60°=2· 　　S△ABC=AB2=×4×3(l2-h2) 　　　　　　　　=3(l2-h2) 　　根据棱锥截面的性质，有 　　 　　∴　S△A‘B’C′=(l2-h2)