题目内容
【题目】已知椭圆C： 
（a＞b＞0）的离心率为
，直线y=x+2过椭圆C的左焦点F1．
（1）求椭圆C的标准方程；
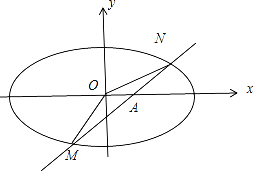
（2）设过点A（0，﹣1）的直线l与椭圆交于不同两点M、N，当△MON的面积为
时，求直线l的方程．
【答案】（1）
（2）y=±x﹣1
【解析】试题分析：（1）根据条件列关于a,b,c方程组，解方程组可得椭圆C的标准方程（2）根据点到直线距离得三角形的高，根据弦长公式得三角形底边边长，根据三角形面积公式列等量关系，解得直线斜率即得直线方程
试题解析：解：（1）∵直线y=x+2过椭圆C的左焦点F1．∴F1（﹣2，0），即c=2．
由离心率e=
，得a=2
，∴b2=a2﹣c2=4
∴椭圆C的标准方程为：
（2）依题意知过点A（0，﹣1）的直线l的斜率一定存在，故设直线l的方程为
y=kx﹣1，
设M（x1，y1），N（x2，y2）
由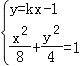
，得（1+2k2）x2﹣4kx﹣6=0
，
S△MON=
=
=
解得k=±1
直线l的方程为：y=±x﹣1
练习册系列答案
相关题目
