题目内容
20.当x为何值时,函数f(x)=$\sqrt{{x}^{2}-2x+2}$+$\sqrt{{x}^{2}-4x+6}$有最小值?并求出最小值.分析 函数化为f(x)=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x-2)^{2}+2}$,根据点与点的距离公式,可以得到几何意义是:x轴上一点C(x,0)到两点A(1,1)、B(2,2)的距离之和.
在x轴另一侧作出点A的对称点,则A1(1,-1),即可求出其最小值,根据两点式求出直线A1B的方程,则方程与x轴的交点的横坐标即可所求的x的值.
解答  解:函数f(x)=$\sqrt{{x}^{2}-2x+2}$+$\sqrt{{x}^{2}-4x+6}$=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x-2)^{2}+2}$,
解:函数f(x)=$\sqrt{{x}^{2}-2x+2}$+$\sqrt{{x}^{2}-4x+6}$=$\sqrt{(x-1)^{2}+1}$+$\sqrt{(x-2)^{2}+2}$,
上式右边的几何意义是:x轴上一点C(x,0)到两点A(1,1)、B(2,2)的距离之和.
在x轴另一侧作出点A的对称点,则A1(1,-1),
∴|CA|+|CB|=|A1B|=$\sqrt{(2-1)^{2}+(2+1)^{2}}$=$\sqrt{10}$,
则点A1,B的直线方程为$\frac{y-2}{2-(-1)}=\frac{x-2}{2-1}$,即y=3x-4,
令y=0.解得x=$\frac{4}{3}$,
故点C的坐标为($\frac{4}{3}$,0),
∴当x=$\frac{4}{3}$时,函数f(x)的最小值为$\sqrt{10}$.
点评 本题考查了点与点的距离公式,直线方程,和最短路线问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列各区间的数轴表示中,正确的是( )
| A. | 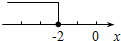 [-2,+∞) | B. | 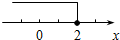 (-∞,2) | C. | 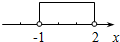 (-1,2) | D. | 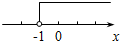 [-1,+∞) |
10.已知集合G={x|-5≤x≤3},H={x|0<x≤7},则G∩H=( )
| A. | {x|-5≤x≤7} | B. | {x|0<x≤3} | C. | {x|-5≤x<0} | D. | {x|3≤x≤7} |