题目内容
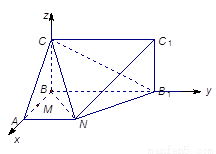
(本小题满分12分)已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明: ⊥平面
⊥平面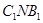 ;
;
(Ⅱ)求平面 与平面
与平面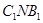 所成角的余弦值;
所成角的余弦值;

【答案】
(10见解析;(2)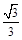 .
.
【解析】(1)由三视图和直观图可得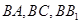 两两垂直,可以
两两垂直,可以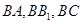 分别为
分别为 轴建立空间直角坐标系,求出点的坐标,利用向量的数量积证明
轴建立空间直角坐标系,求出点的坐标,利用向量的数量积证明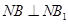 ,
,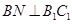 ,由线面垂直的判定定理得
,由线面垂直的判定定理得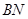 ⊥平面
⊥平面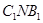 ;(2)在(1)的条件下,分别求出平面
;(2)在(1)的条件下,分别求出平面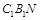 的一个法向量
的一个法向量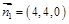 ,平面
,平面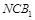 的一个法向量
的一个法向量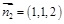 .所以二面角C-NB1-C1的余弦值为
.所以二面角C-NB1-C1的余弦值为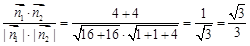 。
。
证明:∵该几何体的正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形, ∴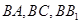 两两垂直.以
两两垂直.以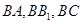 分别为
分别为 轴建立空间直角坐标系如图.--------------2分
轴建立空间直角坐标系如图.--------------2分
则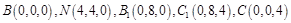 .
.
∴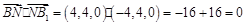 ,
,
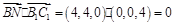 .------------4分
.------------4分
∴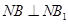 ,
,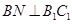 .
.
又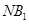 与
与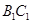 相交于
相交于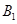 ,
,
∴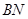 ⊥平面
⊥平面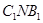 . -------------------6分
. -------------------6分
(Ⅱ)∵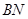 ⊥平面
⊥平面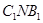 ,
,
∴ 是平面
是平面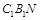 的一个法向量
的一个法向量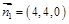 , ------------8分
, ------------8分
设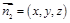 为平面
为平面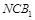 的一个法向量,
的一个法向量,
则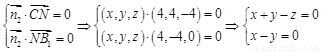 ,
,
所以可取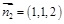 . ------------10分
. ------------10分
则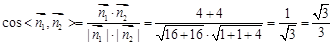 .
.
∴所求二面角C-NB1-C1的余弦值为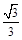 . ------------12分
. ------------12分

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目