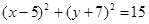题目内容
已知半径为1的动圆与圆(x-5)2+(y+7)2=16外切,则动圆圆心的轨迹方程是( )
分析:由圆(x-5)2+(y+7)2=16的方程找出圆心坐标和半径R,设出所求圆圆心坐标,通过圆心距等于半径和,求出圆的标准方程即可.
解答:解:由圆:(x-5)2+(y+7)2=16,得到圆的圆心坐标为(5,-7),半径R=4,所求圆的半径r=1,
设所求圆的圆心坐标(x,y),两个圆外切时,圆心的轨迹是以(5,-7)为圆心,半径等于R+r=4+1=5的圆,
所求圆的标准方程为:(x-5)2+(y+7)2=25.
综上,动圆圆心的轨迹方程为:(x-5)2+(y+7)2=25.
故选D
设所求圆的圆心坐标(x,y),两个圆外切时,圆心的轨迹是以(5,-7)为圆心,半径等于R+r=4+1=5的圆,
所求圆的标准方程为:(x-5)2+(y+7)2=25.
综上,动圆圆心的轨迹方程为:(x-5)2+(y+7)2=25.
故选D
点评:此题考查学生掌握圆与圆相切时所满足的条件,考查了数形结合的数学思想,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 相切,则动圆圆心的轨迹方程是 ( )
相切,则动圆圆心的轨迹方程是 ( )
 或
或