题目内容
某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值最大?最大日产值为多少?
该厂每天安排生产甲产品5吨,乙产品7吨,则该厂日产值最大,最大日产值为124万元.
解析试题分析:根据已知条件列出线性约束条件,和目标函数。画出可行域与目标函数线,平移目标函数线使之经过可行域,当目标函数线纵截距最大时目标函数值也最大。
试题解析:
设该厂每天安排生产甲产品x吨,乙产品y吨,则日产值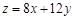 , (1分)
, (1分)
线性约束条件为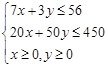 . (4分)
. (4分)
作出可行域. (7分)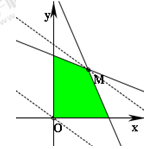
把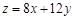 变形为一组平行直线系
变形为一组平行直线系 , (8分)
, (8分)
由图可知,当直线 经过可行域上的点
经过可行域上的点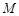 时,截距
时,截距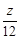 最大,即
最大,即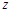 取最大值. (10分)
取最大值. (10分)
解方程组 ,得交点
,得交点 (11分)
(11分)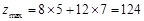 . (13分)
. (13分)
所以,该厂每天安排生产甲产品5吨,乙产品7吨,则该厂日产值最大,最大日产
值为124万元. (14分)
考点:线性规划。

练习册系列答案
相关题目
已知关于 的不等式
的不等式 的解集是
的解集是 ,则关于
,则关于 的不等式
的不等式 的解( )
的解( )
A. | B. | C. | D. |
不等式 <0的解集为( )
<0的解集为( )
| A.{x|﹣2<x<3} | B.{x|x<﹣2} |
| C.{x|x<﹣2或x>3} | D.{x|x>3} |
若规定 =|ad-bc|,则不等式lo
=|ad-bc|,则不等式lo <0的解集为 ( )
<0的解集为 ( )
| A.(0,1) | B.(1,2) |
| C.(0, 2) | D.(0,1)∪(1,2) |
 表示的区域为
表示的区域为 ,不等式
,不等式 表示的平面区域为
表示的平面区域为 .
. =;
=; 为
为 万元投资甲项目,
万元投资甲项目, 万元投资乙项目,试写出
万元投资乙项目,试写出 所表示的平面区域的面积是
所表示的平面区域的面积是  求z的最大值和最小值.
求z的最大值和最小值.