题目内容
在一次商贸交易会上,商家在柜台开展促销抽奖活动,甲、乙两人相约同一天上午去该柜台参与抽奖.
(1)若抽奖规则是从一个装有2个红球和4个白球的袋中无放回地取出2个球,当两个球同色时则中奖,求中奖概率;
(2)若甲计划在9:00~9:40之间赶到,乙计划在9:20~10:00之间赶到,求甲比乙提前到达的概率.
(1)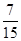 ;(2)
;(2)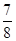
解析试题分析:(1)定义事件A=“中奖”,将6个小球编号,列出从6个小球中不放回地取出2个小球的基本事件总数以及两个球同色时的基本事件数,代入古典概型的概率公式,能正确列出基本事件是解该题的关键,要注意三种取样方法的区别:从6个小球中同时取两个小球有15种,取后放回取两个小球36种、取后不放回有30种;(2)对于几何概型的概率问题,需要正确定义变量,如果涉及一个变量考虑长度的比值;如果涉及两个变量考虑面积的比值;如果三个变量考虑体积的比值,设甲、乙到到的时刻分别为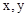 ,列出
,列出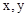 的不等关系,画平面区域,转化为面积的比值.
的不等关系,画平面区域,转化为面积的比值.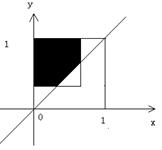
试题解析:(1)记“取到同色球”为事件A,则其概率为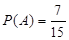 .
.
(2)设甲乙到达的时刻分别为x,y,则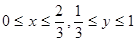 ,甲乙到达时刻(x,y)为图中正方形区域,甲比乙先到则需满足
,甲乙到达时刻(x,y)为图中正方形区域,甲比乙先到则需满足 ,为图中阴影部分区域,设甲比乙先到为事件B,则
,为图中阴影部分区域,设甲比乙先到为事件B,则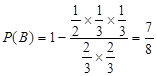
考点:1、古典概型;2、几何概型;3、二元一次不等式表示的平面区域.

练习册系列答案
相关题目
不等式 的解集是
的解集是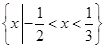 ,则
,则 ( )
( )
A. | B. | C.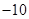 | D. |
若存在实数x使|x-a|+|x-1|≤3成立,则实数a的取值范围是( )
| A.-2≤a≤2 | B.-1≤a≤1 |
| C.-2≤a≤4 | D.-1≤a≤2 |
设函数 ,若
,若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B.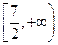 |
C. | D. |
函数y=x2+ (x>0)的最小值是 ( )
(x>0)的最小值是 ( )
A. | B. | C. | D. |

 x-y+
x-y+ 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 ;一个单位的晚餐含
;一个单位的晚餐含 个单位的碳水化合物,
个单位的碳水化合物, 个单位的维生素
个单位的维生素 个单位的碳水化合物,
个单位的碳水化合物, 个单位的蛋白质和
个单位的蛋白质和 个单位的维生素
个单位的维生素 元和
元和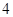 元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
 的最大值为
的最大值为