题目内容
8.已知定义在R上的可导函数为f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+3)为偶函数,f(6)=1,则不等式f(x)<ex的解集为(0,+∞).分析 令g(x)=$\frac{f(x)}{{e}^{x}}$,利用导数和已知即可得出其单调性.再利用函数的对称性和已知可得g(0)=1,从而求得不等式f(x)<ex的解集.
解答 解:设g(x)=$\frac{f(x)}{{e}^{x}}$,则g′(x)=$\frac{{e}^{x}f′(x)-{e}^{x}f(x)}{({e}^{x})^{2}}=\frac{f′(x)-f(x)}{{e}^{x}}$,
∵f′(x)<f(x),∴g′(x)<0.
∴函数g(x)是R上的减函数,
∵函数f(x+3)是偶函数,
∴函数f(-x+3)=f(x+3),
∴函数关于x=3对称,
∴f(0)=f(6)=1,
原不等式等价为g(x)<1,
∴不等式f(x)<ex等价g(x)<1,即g(x)<g(0),
∵g(x)在R上单调递减,
∴x>0.
∴不等式f(x)<ex的解集为(0,+∞).
故答案为:(0,+∞).
点评 本题考查了利用导数研究函数的单调性、利用函数的单调性求解不等式,体现了数学转化思想方法,属于中档题.

练习册系列答案
相关题目
13.由y=$\frac{1}{x}$-2,y=0,x=2所对应的曲线围成的封闭图形的面积为( )
| A. | ln2-1 | B. | 1-ln2 | C. | 2ln2-3 | D. | 3-2ln2 |
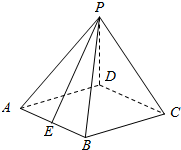 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,平面PED⊥平面PAB,PD⊥AD,点E为AB中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,平面PED⊥平面PAB,PD⊥AD,点E为AB中点.