题目内容

1．已知函数f（x）=x-$\frac{1}{x}$
（1）判断奇偶性；
（2）判断单调性；
（3）求函数的值域．

分析 （1）根据函数f（x）=x-$\frac{1}{x}$的定义域关于原点对称，且f（-x）=-x+$\frac{1}{x}$=-f（x），可得函数f（x）为奇函数．
（2）根据它的导数f′（x）=1+$\frac{1}{{x}^{2}}$＞0，可得函数f（x）在（-∞，0）、（0，+∞）上都是增函数．
（3）在（-∞，0）上，f（x）=x-$\frac{1}{x}$＜0，在（0，+∞）上，f（x）=x-$\frac{1}{x}$＞0，可得函数的值域．

解答 解：（1）函数f（x）=x-$\frac{1}{x}$的定义域为{x|x≠0}，关于原点对称，且f（-x）=-x+$\frac{1}{x}$=-f（x），
故函数f（x）为奇函数．
（2）由于f′（x）=1+$\frac{1}{{x}^{2}}$＞0，故函数f（x）在（-∞，0）、（0，+∞）上都是增函数．
（3）在（-∞，0）∪（0，+∞）上，结合函数f（x）=x-$\frac{1}{x}$ 的图象，如图所示：
可得它的值域为R．

点评 本题主要考查函数的奇偶性的判断、函数的单调性、值域，属于基础题．

练习册系列答案
相关题目
13．若A={1，3，5，7}，B={4，5，7}，则A∩B={5，7}．
12．平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为60°，$\overrightarrow a$=（2，0），|$\overrightarrow b$|=1，则$\overrightarrow b$=$（\frac{1}{2}，±\frac{\sqrt{3}}{2}）$．，|$\overrightarrow a$+2$\overrightarrow b$|=2$\sqrt{3}$．
9．已知点A（1，3）和圆x2+y2=10，以A为中点引线段M1M，其一端点M1沿已知圆周运动，求另一端点M的轨迹方程和轨迹．
16．若圆x2+y2-2y-a=0与圆（x+$\sqrt{3}$）2+y2=1相外切，则a=0．
6．下列函数中，有奇偶性的函数是①②⑤⑥⑦⑧．
①y=ex-e-x②y=lg$\frac{1+x}{1-x}$③y=cos2x ④y=sinx+cosx⑤y=log2（x+$\sqrt{1+{x}^{2}}$）⑥y=$\frac{{e}^{x}-{e}^{-x}}{{e}^{x}+{e}^{-x}}$⑦y=$\frac{{e}^{x}+{e}^{-x}}{{e}^{x}-{e}^{-x}}$⑧y=log2（sinx+$\sqrt{1+si{n}^{2}x}$）⑨y=$\frac{\sqrt{1-{x}^{2}}}{|2-x|+|x+2|}$．
13．求函数f（x）=-2x2+8x+1在区间[t，t+2]的值域．
10．已知定义域在[-1，1]上的函数y=f（x）的值域为[-2，0]，则函数y=f（cos$\sqrt{x}$）的值域是[-2，0]．
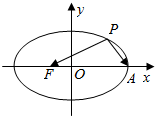11．如图，椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{1}{3}$，F，A分别是椭圆的左焦点和右点顶点，P是椭圆上任意一点，若$\overrightarrow{PF}$•$\overrightarrow{PA}$的最大值是12，则椭圆方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网