题目内容
(本小题满分10分)
设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA.
(Ⅰ)求B的大小;
(Ⅱ)求cosA+sinC的取值范围.
设锐角三角形ABC的内角A,B,C的对边分别为a,b,c,a=2bsinA.
(Ⅰ)求B的大小;
(Ⅱ)求cosA+sinC的取值范围.
(Ⅰ)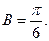
(Ⅱ) 的取值范围为(
的取值范围为(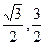 ).
).
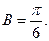
(Ⅱ)
 的取值范围为(
的取值范围为(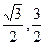 ).
).解:
(I)由 ,根据正弦定理得
,根据正弦定理得
 ,
,
所以 ,
,
由△ABC为锐角的三角形得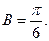
(II)

由△ABC为锐角的三角形知,
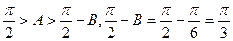 ,
,
所以, ,
,
 ,
,
由此有 ,
,
所以, 的取值范围为(
的取值范围为(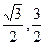 ).
).
(I)由
 ,根据正弦定理得
,根据正弦定理得 ,
,所以
 ,
,由△ABC为锐角的三角形得
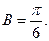
(II)


由△ABC为锐角的三角形知,
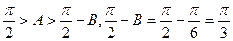 ,
,所以,
 ,
, ,
,由此有
 ,
,所以,
 的取值范围为(
的取值范围为(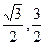 ).
).
练习册系列答案
相关题目
 分别是角A,B,C的对边,
分别是角A,B,C的对边, ,且
,且 ∥
∥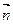
 若
若 ,求
,求 的最大值。
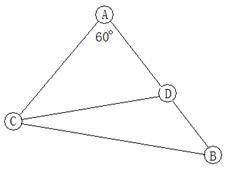
的最大值。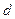 ;②A点处对M、N两点的俯角分别为
;②A点处对M、N两点的俯角分别为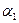 和
和 ;B点处对M、N两点的俯角分别为
;B点处对M、N两点的俯角分别为 和
和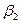 ;请同学们在示意图中标出这四个俯角并用文字和公式写出计算M,N间的距离的步骤.
;请同学们在示意图中标出这四个俯角并用文字和公式写出计算M,N间的距离的步骤.
 (2)在△ABC 中,若AB=2,AC=2BC,求△ABC面积的最大值.
(2)在△ABC 中,若AB=2,AC=2BC,求△ABC面积的最大值.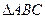 的3个顶点为
的3个顶点为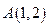 ,
,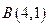 ,
,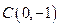 (1)求
(1)求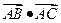 的值;
的值;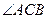 的大小,并判断
的大小,并判断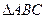 中,
中,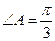 ,
,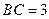 ,
,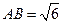 ,则
,则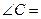 ( )
( )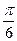
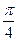
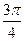
 ,那么PC与平面
,那么PC与平面 ABC所成的角是( )
ABC所成的角是( )
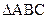 的三边长度分别为3、5、7,则此三角形中最大角的大小为 。
的三边长度分别为3、5、7,则此三角形中最大角的大小为 。