题目内容
(2011•盐城模拟)与直线x=3相切,且与圆(x+1)2+(y+1)2=1相内切的半径最小的圆的方程是
(x-
)2+(y+1)2=
| 1 |
| 2 |
| 25 |
| 4 |
(x-
)2+(y+1)2=
.| 1 |
| 2 |
| 25 |
| 4 |
分析:由题意先确定圆心所在的直线,再求出圆的半径,根据相切求出圆心坐标,再代入圆的标准方程.
解答: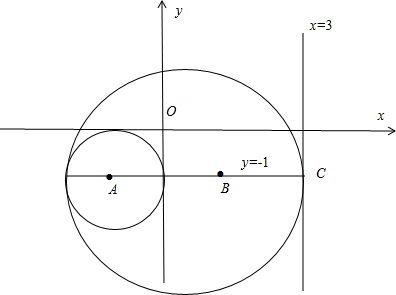 解:由题意知,已知圆的圆心A的坐标(-1,-1),半径R=1,
解:由题意知,已知圆的圆心A的坐标(-1,-1),半径R=1,
设所求的圆心B,则当AB与直线x=3垂直时,即y=-1时所求的圆B的半径r最小;
故设圆心B的坐标(a,-1),
∵所求的圆B与直线x+y-2=0和圆A都相切,
∴a+1=(3-a)-1
∴a=
,r=3-a=
故圆的标准方程是(x-
)2+(y+1)2=
故答案为:(x-
)2+(y+1)2=
 解:由题意知,已知圆的圆心A的坐标(-1,-1),半径R=1,
解:由题意知,已知圆的圆心A的坐标(-1,-1),半径R=1,设所求的圆心B,则当AB与直线x=3垂直时,即y=-1时所求的圆B的半径r最小;
故设圆心B的坐标(a,-1),
∵所求的圆B与直线x+y-2=0和圆A都相切,
∴a+1=(3-a)-1
∴a=
| 1 |
| 2 |
| 5 |
| 2 |
故圆的标准方程是(x-
| 1 |
| 2 |
| 25 |
| 4 |
故答案为:(x-
| 1 |
| 2 |
| 25 |
| 4 |
点评:本题由题意结合图形先判断出圆心的位置,再根据相切的条件求出半径和圆心坐标,考查了数形结合思想和运算能力;求圆的标准方程关键确定出圆心的位置.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 (2011•盐城模拟)如图,已知椭圆
(2011•盐城模拟)如图,已知椭圆 (2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q.
(2011•盐城模拟)(本题文科学生做)如图,在平面直角坐标系xoy中,已知F1(-4,0),F2(4,0),A(0,8),直线y=t(0<t<8)与线段AF1、AF2分别交于点P、Q.