题目内容

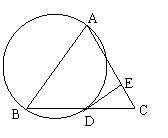 如图，在△ABC中，AB＝AC＝4，BC＝6，以AB为直径的圆交BC于点D，过点D作该圆的切线，交AC于点E，则CE＝.

 

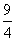【答案】

 .

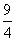【解】设圆心为O，连结OD，AD，则OD⊥DE，AD⊥BC.

因为AB＝AC，所以D为BC的中点，从而OD是△ABC的

中位线，所以OD∥AC，于是AC⊥DE.

在Rt△ADC中，由射影定理，得CD2＝CE·CA.

因为CD＝3，CA＝4，所以CE＝.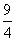

 

练习册系列答案
相关题目
精英家教网如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
AD=4cm．
（1）求：⊙O的直径BE的长；
（2）计算：△ABC的面积．
精英家教网如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=
3
BD，BC=2BD，则sinC的值为（　　）
A、
3
3
B、
3
6
C、
6
3
D、
6
6
如图，在△ABC中，设
AB
=a，
AC
=b，AP的中点为Q，BQ的中点为R，CR的中点恰为P．
（Ⅰ）若
AP
=λa+μb，求λ和μ的值；
（Ⅱ）以AB，AC为邻边，AP为对角线，作平行四边形ANPM，求平行四边形ANPM和三角形ABC的面积之比
S平行四边形ANPM
S△ABC
．
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
（1）求∠ADC的大小；
（2）求AB的长．
如图，在△ABC中，已知
BD
=2
DC
，则
AD
=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网