题目内容
三棱锥S—ABC中,SA⊥底面ABC,SA=4,AB=3,D为AB的中点∠ABC=90°,则点D到面SBC的距离等于
A.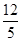 B
B 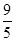 C.
C.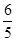 D.
D.
【答案】
C
【解析】略

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
题目内容
三棱锥S—ABC中,SA⊥底面ABC,SA=4,AB=3,D为AB的中点∠ABC=90°,则点D到面SBC的距离等于
A.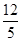 B
B 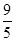 C.
C.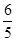 D.
D.
C
【解析】略

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案