题目内容
18.画出下列函数在长度为一个周期的闭区间上的简图(有条件的请用计算器或计算机检验).(1)y=$\frac{1}{2}$sinx;
(2)y=sin3x;
(3)y=sin(x-$\frac{π}{3}$);
(4)y=2sin(2x-$\frac{π}{4}$).
分析 利用五点法进行作图即可.
解答 解:(1)根据题意列出表格得:
| x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| sinx | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y=$\frac{1}{2}$sinx | 0 | $\frac{1}{2}$ | 0 | -$\frac{1}{2}$ | 0 |
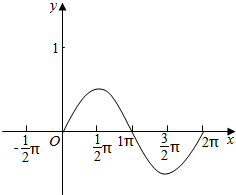
(2):根据题意列出表格得:
| x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| sinx | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y=$\frac{1}{2}$sinx | 0 | $\frac{1}{2}$ | 0 | -$\frac{1}{2}$ | 0 |

(3)根据题意列出表格得:
| x-$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | $\frac{4π}{3}$ | $\frac{11π}{6}$ | $\frac{7π}{3}$ |
| y=sin(x-$\frac{π}{3}$) | 0 | 1 | 0 | -1 | 0 |

(4)根据题意列出表格得:
| 2x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{8}$ | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ |
| y=2sin(2x-$\frac{π}{4}$). | 0 | 2 | 0 | -2 | 0 |

点评 本题主要考查三角函数图象的作图,利用五点法是解决本题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
8.已知数列{an}和{bn}都是等差数列,若a2+b2=3,a4+b4=5,则a7+b7=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
9.已知向量$\overrightarrow{a}$=(m,2),$\overrightarrow{b}$=(3,2m),若$\overrightarrow{a}$•$\overrightarrow{b}$=7,则$\overrightarrow{b}$-$\overrightarrow{a}$等于( )
| A. | (4,4) | B. | (-2,0) | C. | (2,4) | D. | (2,0) |
7.某大学餐饮中心为了解新生的饮食习惯,在全校-年级学生中进行随机抽职了100名学生进行调查.调查结果如表所示:
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)将上述调查所得到学生喜欢甜品的频率视为概率.现在从该大学一年级学生中,采用随机抽样的方法抽职1名学生,抽职5次,记被抽取的5名学生中的“喜欢甜品人数”为X.若每次抽职结果是相互独立的,求期望E(X)和方差D(X).
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(c+d)(b+d)}$,
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | 60 | 10 | 70 |
| 北方学生 | 20 | 10 | 30 |
| 合计 | 80 | 20 | 100 |
(2)将上述调查所得到学生喜欢甜品的频率视为概率.现在从该大学一年级学生中,采用随机抽样的方法抽职1名学生,抽职5次,记被抽取的5名学生中的“喜欢甜品人数”为X.若每次抽职结果是相互独立的,求期望E(X)和方差D(X).
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(a+c)(c+d)(b+d)}$,
| P(K2≥K) | 0.100 | 0.050 | 0.010 |
| K | 2.706 | 3.841 | 6.635 |