题目内容
已知等差数列 的前四项和为10,且
的前四项和为10,且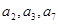 成等比数列
成等比数列
(1)求通项公式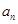
(2)设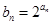 ,求数列
,求数列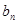 的前
的前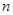 项和
项和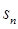 。
。
⑴ ;⑵
;⑵ 或
或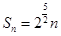 。
。
解析试题分析:(1)利用等差数列的通项公式分别表示出前四项和与a2,a3,a7等比数列关系组成方程组求得a1和d,最后根据等差数列的通项公式求得an.
(2)把(1)中求得的an代入bn=2an中,可知数列{bn}为等比数列,进而根据等比数列的求和公式求得答案.
⑴由题意知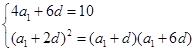

所以 …………6分
…………6分
⑵当 时,数列
时,数列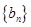 是首项为
是首项为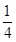 、公比为8的等比数列
、公比为8的等比数列
所以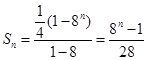 …………9分
…………9分
当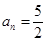 时,
时,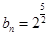 所以
所以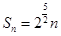
综上,所以 或
或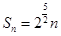 …………12分
…………12分
考点:本题主要考查了等差数列和等比数列的性质.考查了对数列通项公式和求和公式等基本知识的灵活运用.
点评:解决该试题的关键是利用等差数列的通项公式和等比数列的通项公式来求解通项公式,进而结合错位相减法得到求和。

练习册系列答案
相关题目
(本小题满分14分)
已知函数 的图像经过点
的图像经过点 .
.
(1)求该函数的解析式;
(2)数列 中,若
中,若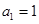 ,
, 为数列
为数列 的前
的前 项和,且满足
项和,且满足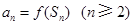 ,
,
证明数列 成等差数列,并求数列
成等差数列,并求数列 的通项公式;
的通项公式;
(3)另有一新数列 ,若将数列
,若将数列 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
 |
  |
   |
    |
 构成的数列即为数列
构成的数列即为数列 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当 时,求上表中第
时,求上表中第 行所有项的和.
行所有项的和. 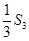 与
与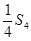 的等比中项为
的等比中项为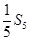 ,
, 的前
的前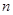 项和为
项和为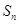 ,且
,且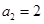 ,
,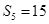 ,数列
,数列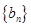 满足:
满足: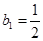 ,
, ,
,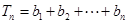 ,
,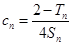 ,证明:
,证明:
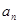 }的前项和为
}的前项和为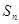 ,且
,且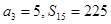 。数列
。数列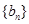 为等比数列,且首项
为等比数列,且首项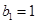 ,
,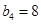 .
.  ,
,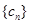 满足
满足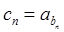 ,求数列
,求数列 项和为
项和为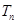 ;
;  为等差数列,且
为等差数列,且 ,
, .
. ,求证:数列
,求证:数列 是等比数列.
是等比数列.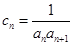 ,求数列
,求数列 的前
的前 项和
项和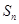 .
.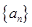 是首项为
是首项为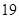 ,公差为
,公差为 的等差数列.
的等差数列.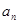 ;
; 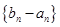 是首项为
是首项为 ,公比为
,公比为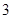 的等比数列,求数列
的等比数列,求数列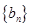 的通项公式及其前
的通项公式及其前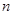 项和
项和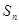 .
.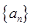 是首项为
是首项为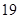 ,公差为
,公差为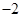 的等差数列,
的等差数列,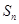 为
为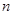 项和.
项和. 及
及 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的通项公式及其前
的通项公式及其前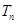 .
.  中,
中, 的前n项和,
的前n项和,
 ,数列
,数列 的前n项和为
的前n项和为 求
求