题目内容
已知函数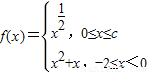
，其中c＞0．且f（x）的值域是[-
，2]，则c的取值范围是 ．
【答案】分析：当0≤x≤c时，可得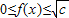
，当-2≤x＜0时，利用函数的单调性可得
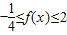，结合分段函数的函数值域的求解可求c的范围
解答：解：当0≤x≤c时，f（x）=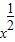
单调递增
∴
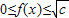
当-2≤x＜0时，f（x）在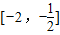
单调递减，在[
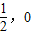）上单调递增
∴
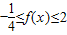
∵f（x）的值域是[-
，2]
∴
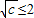
∴0＜c≤4
故答案为：（0，4]
点评：本题主要考查了分段函数的函数值域的求解，解题的关键是利用函数 的单调性及分段函数的函数值域的性质．
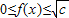，当-2≤x＜0时，利用函数的单调性可得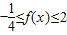，结合分段函数的函数值域的求解可求c的范围解答：解：当0≤x≤c时，f（x）=
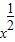单调递增∴
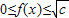
当-2≤x＜0时，f（x）在
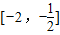单调递减，在[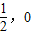）上单调递增∴
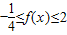
∵f（x）的值域是[-
，2]∴
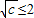
∴0＜c≤4
故答案为：（0，4]
点评：本题主要考查了分段函数的函数值域的求解，解题的关键是利用函数 的单调性及分段函数的函数值域的性质．
练习册系列答案
相关题目
（其中a>0），且
在点（0，0）处的切线与直线
平行。
的两个极值点，且
的取值范围；
，其中c为常数，且函数f（x）图象过原点．
，求函数g（x）的零点．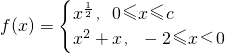
，其中c＞0．且f（x）的值域是[-
，2]，则c的取值范围是________．
（其中a＞0且a≠1），当x≥0且y≥0时，在同一坐标系中画出其中两个函数的大致图象，正确的是（ ）
