题目内容
已知函数 ,其中c为常数,且函数f(x)图象过原点.
,其中c为常数,且函数f(x)图象过原点.(1)求c的值;
(2)证明函数f(x)在[0,2]上是单调递增函数;
(3)已知函数
 ,求函数g(x)的零点.
,求函数g(x)的零点.
【答案】分析:(1)根据函数f(x)图象过原点,即f(0)=0,解得 c的值.
(2)设0≤x1<x2≤2,化简f(x1)-f(x2) 的解析式为-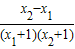 <0,得f(x1)<f(x2 ),从而证明函数f(x)在[0,2]上是单调递增函数.
<0,得f(x1)<f(x2 ),从而证明函数f(x)在[0,2]上是单调递增函数.
(3)令函数 =0,求出x的值,即为函数的零点.
=0,求出x的值,即为函数的零点.
解答:解:(1)∵函数f(x)图象过原点,∴f(0)=0,解得 c=0,故函数f(x)= .
.
(2)证明:设0≤x1<x2≤2,
则f(x1)-f(x2)= -
- =
= =-
=- .
.
由0≤x1<x2≤2 可得,x2-x1>0,x1+1>0,x2+1>0,故有- <0,
<0,
则f(x1)-f(x2)<0,f(x1)<f(x2 ),
故函数f(x)在[0,2]上是单调递增函数.
(3)令 ,
,
∴ ,即x=ln
,即x=ln =-ln2,
=-ln2,
即函数g(x)的零点为 x=-ln2.
点评:本题主要考查函数的单调性的判断和证明,函数零点的定义、求函数零点的方法,属于基础题.
(2)设0≤x1<x2≤2,化简f(x1)-f(x2) 的解析式为-
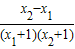 <0,得f(x1)<f(x2 ),从而证明函数f(x)在[0,2]上是单调递增函数.
<0,得f(x1)<f(x2 ),从而证明函数f(x)在[0,2]上是单调递增函数.(3)令函数
 =0,求出x的值,即为函数的零点.
=0,求出x的值,即为函数的零点.解答:解:(1)∵函数f(x)图象过原点,∴f(0)=0,解得 c=0,故函数f(x)=
 .
. (2)证明:设0≤x1<x2≤2,
则f(x1)-f(x2)=
 -
- =
= =-
=- .
.由0≤x1<x2≤2 可得,x2-x1>0,x1+1>0,x2+1>0,故有-
 <0,
<0,则f(x1)-f(x2)<0,f(x1)<f(x2 ),
故函数f(x)在[0,2]上是单调递增函数.
(3)令
 ,
,∴
 ,即x=ln
,即x=ln =-ln2,
=-ln2,即函数g(x)的零点为 x=-ln2.
点评:本题主要考查函数的单调性的判断和证明,函数零点的定义、求函数零点的方法,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
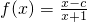 ,其中c为常数,且函数f(x)图象过原点.
,其中c为常数,且函数f(x)图象过原点.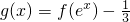 ,求函数g(x)的零点.
,求函数g(x)的零点. ,其中a为常数.则“
,其中a为常数.则“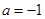 ”是f(x)为奇函数”的
”是f(x)为奇函数”的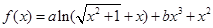 ,其中
,其中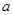 、
、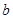 为常数,
为常数,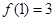 ,则
,则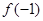 =_____________.
=_____________.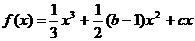 (b、c为常数).
(b、c为常数).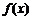 在
在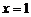 和
和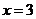 处取得极值,试求
处取得极值,试求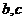 的值;
的值;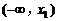 、
、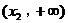 上单调递增,且在
上单调递增,且在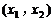 上单调递减,又满足
上单调递减,又满足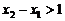 ,求证:
,求证: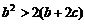 。
。