题目内容
设函数f(x)= -sin(2x-
-sin(2x- ).
).
(I)求函数f(x)的最大值和最小值;
(Ⅱ)△ABC的内角A,B,C的对边分别为a,b,c,c=3,f(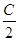 )=
)= ,若
,若 ,求△ABC的面积.
,求△ABC的面积.
【答案】
(I)函数取得最大值1,函数取得最小值0;(Ⅱ)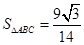 .
.
【解析】
试题分析:(I)求函数 的最大值与最小值,需将函数
的最大值与最小值,需将函数 转化为一个角的一个三角函数,因此需对
转化为一个角的一个三角函数,因此需对 降次整理,此题降次后,以及sin(2x-
降次整理,此题降次后,以及sin(2x- )利用诱导公式,转化为
)利用诱导公式,转化为 ,从而求解;(Ⅱ)求△ABC的面积,由三角形面积公式
,从而求解;(Ⅱ)求△ABC的面积,由三角形面积公式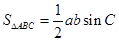 ,须知道
,须知道 ,及
,及 的值,由
的值,由 来确定
来确定 的值,由
的值,由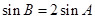 ,可利用正弦定理转化为
,可利用正弦定理转化为 的关系,再由余弦定理,求出
的关系,再由余弦定理,求出 的值,从而求解.
的值,从而求解.
试题解析:(I)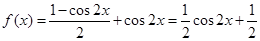 ∴当
∴当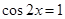 时,函数取得最大值1;当
时,函数取得最大值1;当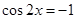 时,函数取得最小值0;
时,函数取得最小值0;
(Ⅱ)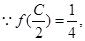
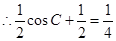 ,又
,又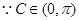 ,
,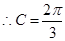 ,
,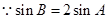 ,
,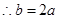 ,
,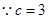 ,
,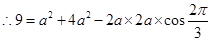 ,
,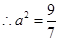 ,
,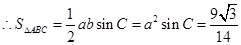
考点:三角恒等变化,正弦定理、余弦定理在解三角形中的应用,考查学生数形结合的能力以及转化与化归能力.

练习册系列答案
相关题目