题目内容
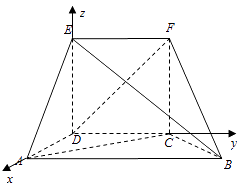
【题目】如图,几何体EF﹣ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°. 
(1)求证:AC⊥FB
(2)求二面角E﹣FB﹣C的大小.
【答案】
(1)证明:由题意得,AD⊥DC,AD⊥DF,且DC∩DF=D,
∴AD⊥平面CDEF,∴AD⊥FC,
∵四边形CDEF为正方形.∴DC⊥FC
由DC∩AD=D∴FC⊥平面ABCD,∴FC⊥AC
又∵四边形ABCD为直角梯形,
AB∥CD,AD⊥DC,AD=2,AB=4
∴ ![]() ,
, ![]() ,则有AC2+BC2=AB2
,则有AC2+BC2=AB2
∴AC⊥BC
由BC∩FC=C,∴AC⊥平面FCB,∴AC⊥FB
(2)解:由(1)知AD,DC,DE所在直线相互垂直,
故以D为原点,DA,DC,DE所在直线分别为x,y,z轴,
建立如图所示的空间直角坐标系,
可得D(0,0,0),F(0,2,2),B(2,4,0),
E(0,0,2),C(0,2,0),A(2,0,0),
由(1)知平面FCB的法向量为 ![]() ,
,
∴ ![]() ,
,
设平面EFB的法向量为 ![]() ,
,
则有: 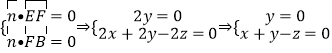
令z=1则 ![]() ,
,
设二面角E﹣FB﹣C的大小为θ,
![]() ,
,
∵ ![]() ,∴
,∴ ![]() .
.
【解析】(1)由题意得,AD⊥DC,AD⊥DF,从而AD⊥FC,DC⊥FC,由此能证明AC⊥FB.(2)以D为原点,DA,DC,DE所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角E﹣FB﹣C的大小.

【题目】某宾馆有![]() 间标准相同的客房,客房的定价将影响入住率.经调查分析,得出每间客房的定价与每天的入住率的大致关系如下表:
间标准相同的客房,客房的定价将影响入住率.经调查分析,得出每间客房的定价与每天的入住率的大致关系如下表:
每间客房的定价 | 220元 | 200元 | 180元 | 160元 |
每天的入住率 |
|
|
|
|
对于每间客房,若有客住,则成本为80元;若空闲,则成本为40元.要使此宾馆每天的住房利润最高,则每间客房的定价大致应为( )
A. 220元 B. 200元 C. 180元 D. 160元