题目内容
)已知函数 满足对一切
满足对一切 都有
都有 ,且
,且 ,当
,当 时有
时有 .
.
(1)求 的值;
的值;
(2)判断并证明函数 在
在 上的单调性;
上的单调性;
(3)解不等式:
【答案】
⑴令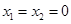 ,得
,得  ,
,

再令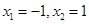 ,得
,得  ,
,
即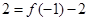 ,从而
,从而 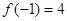 .
---------------------------------2分
.
---------------------------------2分
⑵任取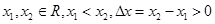
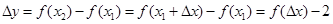 -------------------4分
-------------------4分

 .
-------------6分
.
-------------6分
 ,即
,即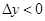 .
.
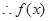 在
在 上是减函数.
-------------------------------------------8分
上是减函数.
-------------------------------------------8分
⑶由条件知,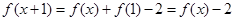 ,
,
设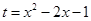 ,则
,则 ,即
,即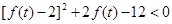 ,
,
整理,得  ,
-------------------9分
,
-------------------9分
而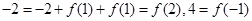 ,
,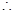 不等式即为
不等式即为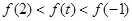 ,
,
又因为 在
在 上是减函数,
上是减函数,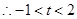 ,即
,即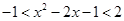 , ---------11分
, ---------11分
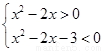 ,从而所求不等式的解集为
,从而所求不等式的解集为 .
.
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
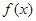 满足对一切
满足对一切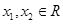 都有
都有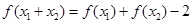 ,且
,且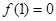 ,当
,当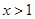 时有
时有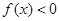 .
.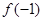 的值;
的值;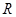 上的单调性;
上的单调性;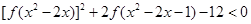 .
.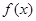 满足对一切
满足对一切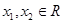 都有
都有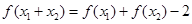 ,且
,且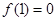 ,
,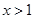 时有
时有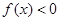 .
.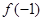 的值;
的值;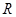 上的单调性;
上的单调性;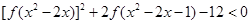 .
.