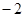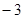题目内容
等差数列中,若a3+a4+a5+a6+a7+a8+a9=420,则a2+a10=( )
| A.100 | B.120 | C.140 | D. 160 |
B
试题分析:根据等差数列的性质可知,由a3+a4+a5+a6+a7+a8+a9=(a3+a9)+(a4+a8)+(a5+a7)+a6=7a6=420,得到a6=60,则a2+a12=2a6=120.故选B
点评:解决该试题的关键是根据等差数列的性质可知,项数之和相等的两项之和相等,化简已知的等式即可求出a5的值,然后把所求的式子也利用等差数列的性质化简后,将a5的值代入即可求出值.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
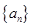 的前
的前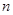 项和为
项和为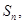
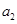 、
、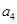 是方程
是方程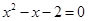 的两个根,则
的两个根,则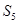 等于 .
等于 .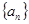 中,
中,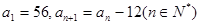 .则
.则 。
。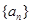 的前10项中,所有偶数项、所有奇数项之和分别为55和45,则它的首项
的前10项中,所有偶数项、所有奇数项之和分别为55和45,则它的首项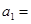 _______。
_______。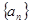 的通项为
的通项为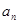 =
=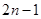 ,
,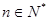 ,其前
,其前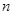 项和为
项和为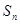 ,则使
,则使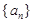 中,
中,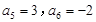 ,则公差d为 .
,则公差d为 . 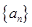 中,
中,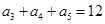 ,那么
,那么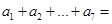
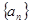 的通项公式为
的通项公式为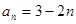 ,则它的公差为( )
,则它的公差为( )