题目内容
设奇函数f（x）的定义域为R，最小正周期T=3，若f(1)≥1，f(2)=
，则a的取值范围是（ ）
| 2a-3 |
| a+1 |
A、a＜-1或a≥
| ||
| B、a＜-1 | ||
C、-1＜a≤
| ||
D、a≤
|
分析：关键函数是一个奇函数和具有周期性，得到2对应的函数值与-1对应的函数的范围一样，列出关于a的不等式，解不等式即可．
解答：解：∵奇函数f（x）的定义域为R，
∴f（-1）=-f（1）≤-1，
∵最小正周期T=3，若f(1)≥1，f(2)=
，
∴f（2）=f（-1）≤-1，
∴
≤-1，
∴（a+1）（3a-2）≤0，
∴-1≤a≤
，且a+1≠0，
∴-1＜a≤
故选C．
∴f（-1）=-f（1）≤-1，
∵最小正周期T=3，若f(1)≥1，f(2)=
| 2a-3 |
| a+1 |
∴f（2）=f（-1）≤-1，
∴
| 2a-3 |
| a+1 |
∴（a+1）（3a-2）≤0，
∴-1≤a≤
| 2 |
| 3 |
∴-1＜a≤
| 2 |
| 3 |
故选C．
点评：本题考查函数的性质，是一个函数性质的综合应用，解题的关键是把2对应的函数值同已知条件结合起来．
练习册系列答案
名校课堂系列答案
相关题目
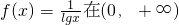是减函数；
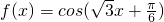，则f（x）+f'（x）是奇函数；
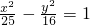的一个焦点到渐近线的距离是5；
是减函数；
，则f（x）+f'（x）是奇函数；
的一个焦点到渐近线的距离是5；