题目内容
 ,<
,<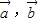 >=
>=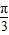 ,且(
,且(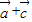 )(
)(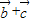 )=
)= ,则|
,则|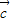 |取值范围( )
|取值范围( )A.[-
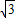 ,
,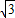 ]
]B.[0,
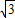 ]
]C.(0,
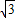 ]
]D.[0,
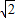 ]
]
【答案】分析:利用向量的数量积公式和向量加法的三角形法则得到 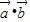 ,
,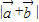 ;利用向量的数量积的运算律将
;利用向量的数量积的运算律将 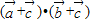 展开,利用三角函数的有界性求出取值范围.
展开,利用三角函数的有界性求出取值范围.
解答:解:根据已知得: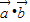 =
= 且
且 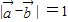 ,
,
由于(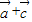 )(
)(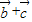 )=
)=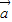 •
•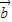 +
+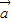 •
•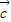 +
+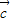 •
•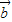 +
+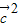 =(
=( 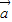 +
+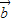 )•
)•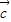 +
+ +
+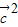 ,
,
且(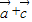 )(
)(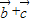 )=
)= ,
,
∴-(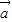 +
+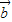 )•
)•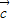 =
=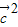
设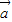 +
+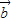 与
与 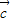 的夹角为θ,
的夹角为θ,
则(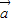 +
+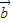 )•
)•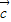 =|
=|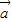 +
+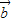 ||
|| |cosθ
|cosθ
故|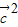 |=-|
|=-|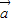 +
+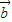 ||
||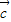 |cosθ
|cosθ
|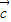 |=-|
|=-|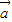 +
+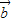 |cosθ,
|cosθ,
又∵(|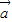 +
+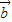 |)2=
|)2=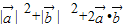 =3,
=3,
∴|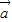 +
+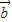 |=
|=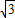
∵-1≤cosθ≤1
∴则|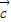 |取值范围[0,
|取值范围[0,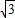 ]
]
故选B.
点评:本题考查向量的数量积公式、向量的运算法则、三角函数的有界性,是中档题.
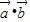 ,
,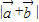 ;利用向量的数量积的运算律将
;利用向量的数量积的运算律将 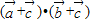 展开,利用三角函数的有界性求出取值范围.
展开,利用三角函数的有界性求出取值范围.解答:解:根据已知得:
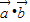 =
= 且
且 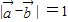 ,
,由于(
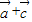 )(
)(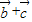 )=
)=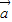 •
•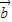 +
+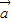 •
•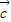 +
+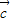 •
•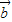 +
+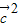 =(
=( 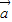 +
+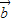 )•
)•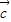 +
+ +
+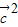 ,
,且(
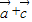 )(
)(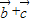 )=
)= ,
,∴-(
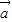 +
+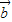 )•
)•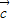 =
=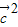
设
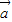 +
+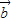 与
与 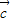 的夹角为θ,
的夹角为θ,则(
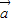 +
+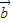 )•
)•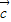 =|
=|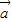 +
+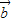 ||
|| |cosθ
|cosθ故|
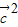 |=-|
|=-|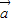 +
+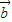 ||
||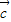 |cosθ
|cosθ|
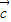 |=-|
|=-|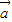 +
+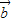 |cosθ,
|cosθ,又∵(|
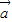 +
+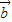 |)2=
|)2=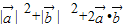 =3,
=3,∴|
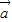 +
+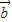 |=
|=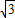
∵-1≤cosθ≤1
∴则|
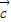 |取值范围[0,
|取值范围[0,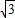 ]
]故选B.
点评:本题考查向量的数量积公式、向量的运算法则、三角函数的有界性,是中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
设
、
、
是单位向量,且
•
=0,则(
-
)•(
-
)的最小值为( )
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
| A、-2 | ||
B、
| ||
| C、-1 | ||
D、1-
|
已知函数f(x)=sin(ωx-
)(ω>0),f(
)+f(
)=0,且f(x)在区间(
,
)单调递减,则ω的值为( )
| 3π |
| 4 |
| 5π |
| 8 |
| 9π |
| 8 |
| 5π |
| 8 |
| 9π |
| 8 |
| A、2 | ||||
B、
| ||||
C、2或
| ||||
D、
|