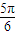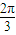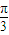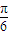题目内容
若向量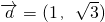 ,|
,| |=1,且(
|=1,且( )•
)• =0,则
=0,则 与
与 的夹角为
的夹角为
- A.

- B.

- C.

- D.

C
分析:先将( )•
)• =0展开将|
=0展开将| |=1代入,求出所
|=1代入,求出所 ,利用向量的数量积公式求出cosθ=
,利用向量的数量积公式求出cosθ= ,求出向量的夹角.
,求出向量的夹角.
解答:设 与
与 的夹角为θ
的夹角为θ
因为( )•
)• =0,
=0,
所以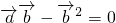 ,
,
因为| |=1,
|=1,
所以 ,
,
所以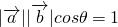 ,
,
因为向量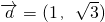 ,|
,|
所以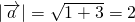
所以2×1cosθ=1,
所以cosθ=
所以 ,
,
故选C.
点评:本题考查利用向量的数量积公式求向量的夹角;考查向量的模的平方等于向量的平方,属于基础题.
分析:先将(
 )•
)• =0展开将|
=0展开将| |=1代入,求出所
|=1代入,求出所 ,利用向量的数量积公式求出cosθ=
,利用向量的数量积公式求出cosθ= ,求出向量的夹角.
,求出向量的夹角.解答:设
 与
与 的夹角为θ
的夹角为θ因为(
 )•
)• =0,
=0,所以
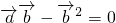 ,
,因为|
 |=1,
|=1,所以
 ,
,所以
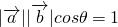 ,
,因为向量
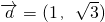 ,|
,|所以
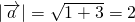
所以2×1cosθ=1,
所以cosθ=

所以
 ,
,故选C.
点评:本题考查利用向量的数量积公式求向量的夹角;考查向量的模的平方等于向量的平方,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若向量
=(1,2),
=(-3,2)且(k
+
)∥(
-3
)则实数k=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、-
| ||
| B、-2 | ||
C、
| ||
D、
|
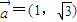 ,|
,| |=1,且(
|=1,且(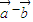 )•
)•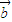 =0,则
=0,则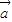 与
与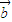 的夹角为( )
的夹角为( )