题目内容
函数f（x）=x3-ax2-bx+a2在x=1处有极值10，则点（a，b）为（ ）A．（3，-3）
B．（-4，11）
C．（3，-3）或（-4，11）
D．不存在
【答案】分析：首先对f（x）求导，然后由题设在x=1时有极值10可得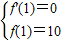 
解之即可求出a和b的值．
解答：解：对函数f（x）求导得 f′（x）=3x2-2ax-b，
又∵在x=1时f（x）有极值10，
∴
，
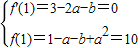解得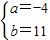
或 
，
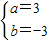验证知，当a=3，b=-3时，在x=1无极值，
故选B．
点评：掌握函数极值存在的条件，考查利用函数的极值存在的条件求参数的能力，属于中档题．
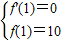解之即可求出a和b的值．解答：解：对函数f（x）求导得 f′（x）=3x2-2ax-b，
又∵在x=1时f（x）有极值10，
∴
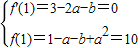，解得
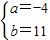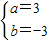或 ，验证知，当a=3，b=-3时，在x=1无极值，
故选B．
点评：掌握函数极值存在的条件，考查利用函数的极值存在的条件求参数的能力，属于中档题．
练习册系列答案
芝麻开花课程新体验系列答案
怎样学好牛津英语系列答案
相关题目