题目内容
对于函数f（x）=x3+ax2-x+1的极值情况，4位同学有下列说法：甲：该函数必有2个极值；乙：该函数的极大值必大于1；丙：该函数的极小值必小于1；丁：方程f（x）=0一定有三个不等的实数根． 这四种说法中，正确的个数是（ ）
分析：f′（x）=3x2+2ax-1，显然，判别式（2a）2-4×3×（-1）=4a2+12＞0，故f′（x）有两个不相等的零点x1，x2，且一正一负，不妨设0＜x1＜x2．f（x）=x3+ax2-x+1图象必过点（0，1），函数f（x）=x3+ax2-x+1在（-∞，x1）上递增，（x1，x2）上递减，（x2，+∞）上递增，可画出函数的图象，可得答案．
解答：解：f（x）=x3+ax2-x+1，则f′（x）=3x2+2ax-1，显然，判别式（2a）2-4×3×（-1）=4a2+12＞0，
故f′（x）有两个不相等的零点x1，x2，且一正一负，不妨设x1＜0＜x2．又f（x）=x3+ax2-x+1图象必过点（0，1）
二次函数f′（x）=3x2+2ax-1，开口向上，且在（-∞，x1）上为正，（x1，x2）上为负，（x2，+∞）上为正，
即函数f（x）=x3+ax2-x+1在（-∞，x1）上递增，（x1，x2）上递减，（x2，+∞）上递增．
由极值的定义可知：函数f（x）必有两个极值点，且x=x1处是极大值点，x=x2处是极小值点．
由以上性质作函数f（x）=x3+ax2-x+1的图象
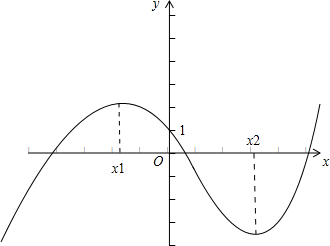或
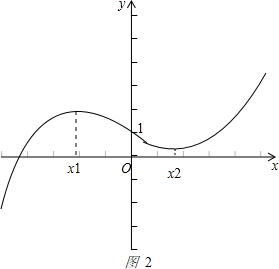
由图1，图2可知：甲正确；乙正确；丙正确；丁不正确．
故选C．
故f′（x）有两个不相等的零点x1，x2，且一正一负，不妨设x1＜0＜x2．又f（x）=x3+ax2-x+1图象必过点（0，1）
二次函数f′（x）=3x2+2ax-1，开口向上，且在（-∞，x1）上为正，（x1，x2）上为负，（x2，+∞）上为正，
即函数f（x）=x3+ax2-x+1在（-∞，x1）上递增，（x1，x2）上递减，（x2，+∞）上递增．
由极值的定义可知：函数f（x）必有两个极值点，且x=x1处是极大值点，x=x2处是极小值点．
由以上性质作函数f（x）=x3+ax2-x+1的图象
或由图1，图2可知：甲正确；乙正确；丙正确；丁不正确．
故选C．
点评：本题为函数极值的问题，利用导数研究函数的性质，进而得出函数的图象是解决问题的关键，属基础题．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
设函数f（x）的定义域为A，若存在非零实数t，使得对于任意x∈C（C⊆A），有x+t∈A，且f（x+t）≤f（x），则称f（x）为C上的t低调函数．如果定义域为[0，+∞）的函数f（x）=-|x-m2|+m2，且 f（x）为[0，+∞）上的10低调函数，那么实数m的取值范围是（ ）
| A、[-5，5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|