题目内容
【题目】某闯关游戏规划是:先后掷两枚骰子,将此试验重复![]() 轮,第
轮,第![]() 轮的点数分别记为
轮的点数分别记为![]() ,如果点数满足
,如果点数满足![]() ,则认为第
,则认为第![]() 轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
(1)求第1轮闯关成功的概率;
(2)如果第![]() 轮闯关成功所获的奖金(单位:元)
轮闯关成功所获的奖金(单位:元) ![]() ,求某人闯关获得奖金不超过2500元的概率;
,求某人闯关获得奖金不超过2500元的概率;
(3)如果游戏只进行到第4轮,第4轮后无论游戏成功与否,都终止游戏,记进行的轮数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】
(1)枚举法列出所有满足条件的数对![]() 即可;
即可;
(2)由![]() ,得
,得![]() ,由(1)每轮过关的概率为
,由(1)每轮过关的概率为![]() ,某人闯关获得奖金不超过2500元的概率:
,某人闯关获得奖金不超过2500元的概率:![]() ;
;
(3)设游戏第![]() 轮后终止的概率为
轮后终止的概率为![]() ,分别求出相应的概率,由此能求出X的分布列和数学期望.
,分别求出相应的概率,由此能求出X的分布列和数学期望.
解:(1)若第1轮闯关成功,
当![]() 时,
时, ![]() ,因此
,因此![]() ;
;
当![]() 时,
时, ![]() ,因此
,因此![]() ;
;
当![]() 时,
时,![]() ,因此
,因此![]() ;
;
当![]() 时,
时,![]() ,因此
,因此![]() ;
;
当![]() 时,
时, ![]() ,因此
,因此![]() ;
;
当![]() 时,
时, ![]() ,因此
,因此![]() 无值.
无值.
记“第1轮闯关成功”为事件![]() ,
,
则第1轮闯关成功的概率![]() .
.
(2)由![]() ,得
,得![]() ,
,
由(1)知每轮闯关成功的概率为![]() .
.
某人闯关获得奖金不超过2500元的概率![]()
![]() .
.
(3)依题意![]() 的所有可能取值为1,2,3,4,
的所有可能取值为1,2,3,4,
设游戏第![]() 轮后终止的概率为
轮后终止的概率为![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
![]() .
.
故![]() 的分布列为
的分布列为
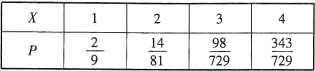
因此数学期望![]()
![]() .
.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
【题目】某市2016年6月30天的空气质量指数如下:
35 | 54 | 80 | 86 | 72 | 85 | 58 | 125 | 111 | 53 |
10 | 66 | 46 | 36 | 18 | 25 | 23 | 40 | 60 | 89 |
88 | 54 | 79 | 14 | 16 | 40 | 59 | 67 | 111 | 62 |
你觉得这个月的空气质量如何?请设计适当的频率分布直方图展示这组数据,并结合空气质量分级标准分析数据.

