题目内容
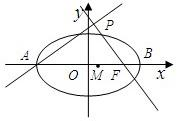
 如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方,
如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方,| PA |
| PF |
(Ⅰ)求椭圆的方程和离心率;
(Ⅱ)求点P的坐标;
(Ⅲ)若过点F且倾斜角为45°的直线l交椭圆于D,E两点,求△ADE的面积.
分析:(I)确定a,c的值,即可求出椭圆的离心率,及椭圆的方程;
(II)利用点P在椭圆上且位于x轴上方,
•
=0,即可求出P的坐标;
(III)直线方程代入椭圆方程,利用韦达定理,结合三角形的面积公式,可得结论.
(II)利用点P在椭圆上且位于x轴上方,
| PA |
| PF |
(III)直线方程代入椭圆方程,利用韦达定理,结合三角形的面积公式,可得结论.
解答:解:(Ⅰ)由题意知a=6,c=4,∴e=
=
=
…(1分)
∴b2=a2-c2=36-16=20…(2分)
∴椭圆方程为
+
=1…(3分)
(Ⅱ)设点P的坐标是(x,y),则
=(x+6,y),
=(x-4,y)…(4分)
由已知得
…(5分)
则2x2+9x-18=0,x=
或x=-6…(7分)
由于y>0,只能x=
,于是y=
…(8分)
所以点P的坐标是(
,
)…(9分)
(Ⅲ)∵l的倾斜角为45°,∴l的斜率k=1
∴l:y=x-4⇒x=y+4,
若设D(x1,y1),E(x2,y2)…(10分)
联立:
⇒7y2+20y-50=0,…(11分)
则|y1-y2|=
=
…(12分)
显然S△ADE=S△AFD+S△AFE=
|AF|×|y1-y2|=
×10×
=
∴△ADE的面积为
.…(13分)
| c |
| a |
| 4 |
| 6 |
| 2 |
| 3 |
∴b2=a2-c2=36-16=20…(2分)
∴椭圆方程为
| x2 |
| 36 |
| y2 |
| 20 |
(Ⅱ)设点P的坐标是(x,y),则
| AP |
| FP |
由已知得
|
则2x2+9x-18=0,x=
| 3 |
| 2 |
由于y>0,只能x=
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
所以点P的坐标是(
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
(Ⅲ)∵l的倾斜角为45°,∴l的斜率k=1
∴l:y=x-4⇒x=y+4,
若设D(x1,y1),E(x2,y2)…(10分)
联立:
|
则|y1-y2|=
| ||
| 7 |
30
| ||
| 7 |
显然S△ADE=S△AFD+S△AFE=
| 1 |
| 2 |
| 1 |
| 2 |
30
| ||
| 7 |
150
| ||
| 7 |
∴△ADE的面积为
150
| ||
| 7 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,点A,B分别是椭圆
如图,点A,B分别是椭圆 如图,点A、B分别是椭圆
如图,点A、B分别是椭圆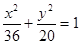 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于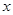 轴上方,
轴上方,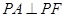 .
.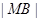 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离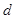 的最小值.
的最小值.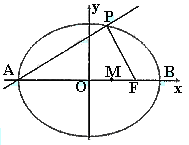
 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为: 且
且 。
。
 ,求椭圆上的点到
,求椭圆上的点到