题目内容
4.先作图,观察以A、B、C为顶点的三角形的形状,然后给出证明:(1)A(-1,-4),B(5,2),C(3,4);
(2)A(-2,-3),B(19,4),C(-1,-6).
分析 作图,利用斜率关系,判断三角形的形状.
解答 解:(1)如图所示,kBC=$\frac{4-2}{3-5}$=-1,kAB=$\frac{2+4}{5+1}$=1,
∴BC⊥AB,
∴△ABC是直角三角形;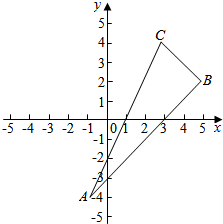
(2)如图所示,kAC=$\frac{-3+6}{-2+1}$=-3,kAB=$\frac{4+3}{19+2}$=$\frac{1}{3}$,
∴AC⊥AB,
∴△ABC是直角三角形;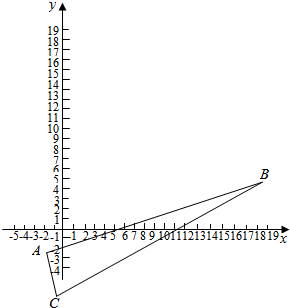
点评 本题考查判断三角形的形状,考查数形结合的数学思想,比较基础.

练习册系列答案
相关题目
6.已知f($\sqrt{x}$+4)=x+8$\sqrt{x}$,则f(x2)=( )
| A. | x4-16(x≤-2或x≥2) | B. | x4-16(-2≤x≤2) | C. | x2-16(x≤-2或x≥2) | D. | x2-16(-2≤x≤2) |
16.在△ABC中,a、b、c分别为角A、B、C的对边,若∠B=$\frac{π}{6}$,b=1,c=2,则a=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{7}$ |
14.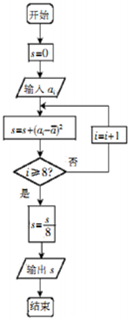 如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
 如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| 39 | 40 | 42 | 42 | 43 | 45 | 46 | 47 |
| A. | A | B. | B | C. | C | D. | D |