题目内容
已知圆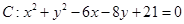 ,直线
,直线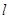 过定点
过定点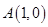 .
.
(1)求圆心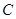 的坐标和圆的半径
的坐标和圆的半径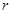 ;
;
(2)若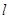 与圆C相切,求
与圆C相切,求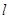 的方程;
的方程;
(3)若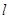 与圆C相交于P,Q两点,求三角形
与圆C相交于P,Q两点,求三角形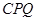 面积的最大值,并求此时
面积的最大值,并求此时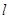 的直线方程.
的直线方程.
【答案】
(1)圆心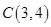 ,半径
,半径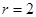 (2)
(2)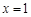 或
或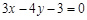 (3)
(3) 或
或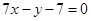
【解析】
试题分析:(1)将圆的一般方程化为标准方程,得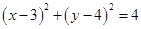
∴圆心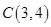 ,半径
,半径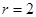 .
2分
.
2分
(2)①若直线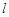 的斜率不存在,则直线
的斜率不存在,则直线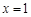 ,符合题意.
3分
,符合题意.
3分
②若直线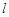 斜率存在,设直线
斜率存在,设直线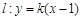 ,即
,即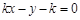 .
.
∵ 与圆
与圆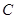 相切.
相切.
∴圆心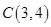 到已知直线
到已知直线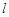 的距离等于半径2,即
的距离等于半径2,即
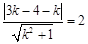 4分
4分
解得 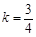 .
5分
.
5分
∴综上,所求直线方程为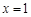 或
或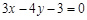 . 6分
. 6分
(3)直线与圆相交,斜率必定存在,设直线方程为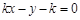 .
.
则圆心到直线l的距离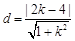 7分
7分
又∵ 面积
面积 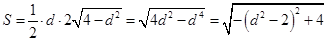 9分
9分
∴当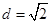 时,
时,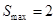 .
10分
.
10分
由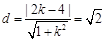 ,解得
,解得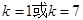 11分
11分
∴直线方程为 或
或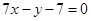 .
12分
.
12分
考点:圆的方程与直线与圆相切相交的位置关系
点评:过圆外一点的圆的切线有两条,当用点斜式求出的切线只有一条时,另一条切线斜率不存在;当直线与圆相交时,圆心到直线的距离,弦长的一半及圆的半径构成直角三角形,此三角形在求解直线与圆相交时经常用到

练习册系列答案
相关题目
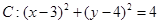 ,直线
,直线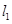 过定点A(1,0),若
过定点A(1,0),若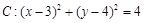 ,直线
,直线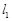 过定点
A (1,0).
过定点
A (1,0).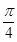 ,
, ,直线
,直线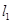 过定点A(1,0).
过定点A(1,0).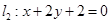 的交点为N,求证:
的交点为N,求证: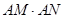 为定值.
为定值.