题目内容
已知函数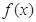 =
=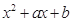 ,
,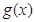 =
=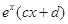 ,若曲线
,若曲线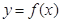 和曲线
和曲线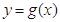 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线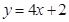 .
.
(Ⅰ)求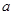 ,
,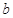 ,
,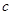 ,
,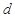 的值;
的值;
(Ⅱ)若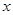 ≥-2时,
≥-2时, ≤
≤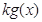 ,求
,求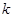 的取值范围.
的取值范围.
【答案】
(Ⅰ)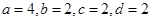 ;
(Ⅱ)
;
(Ⅱ) 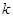 的取值范围为[1,
的取值范围为[1,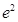 ].
].
【解析】
试题分析:(Ⅰ)先由过点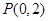 得出
得出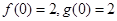 ,再求在点
,再求在点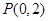 导数,由导数几何意义知
导数,由导数几何意义知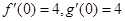 ,从而解得
,从而解得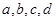 ;
;
(Ⅱ)设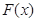 =
=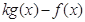 =
=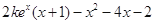 (
(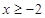 )
)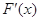 =
=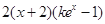 ,
由题设可得
,
由题设可得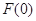 ≥0,即
≥0,即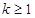 , 令
, 令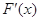 =0得,
=0得,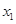 =
=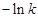 ,
,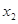 =-2,
对
=-2,
对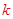 分3中情况讨论得出结果.
分3中情况讨论得出结果.
试题解析:(Ⅰ)由已知得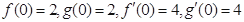 ,
,
而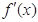 =
=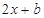 ,
,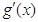 =
=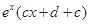 ,∴
,∴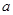 =4,
=4,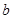 =2,
=2,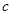 =2,
=2,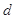 =2;
=2;
(Ⅱ)由(Ⅰ)知,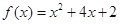 ,
,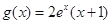 ,
设函数
,
设函数
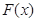 =
=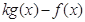 =
=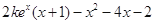 (
(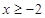 ),
),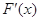 =
=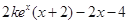 =
=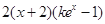 ,
由题设可得
,
由题设可得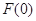 ≥0,即
≥0,即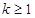 , 令
, 令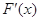 =0得,
=0得,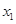 =
=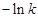 ,
,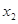 =-2,
=-2,
(1)若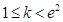 ,则-2<
,则-2<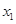 ≤0,∴当
≤0,∴当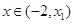 时,
时,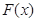 <0,当
<0,当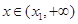 时,
时,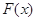 >0,即
>0,即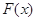 在
在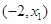 单调递减,在
单调递减,在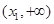 单调递增,故
单调递增,故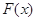 在
在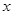 =
=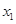 取最小值
取最小值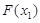 ,而
,而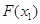 =
= =
=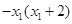 ≥0,
∴当
≥0,
∴当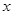 ≥-2时,
≥-2时,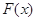 ≥0,即
≥0,即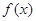 ≤
≤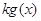 恒成立,
恒成立,
(2)若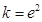 ,则
,则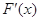 =
=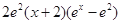 ,
∴当
,
∴当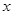 ≥-2时,
≥-2时,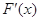 ≥0,∴
≥0,∴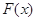 在(-2,+∞)单调递增,而
在(-2,+∞)单调递增,而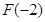 =0, ∴当
=0, ∴当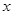 ≥-2时,
≥-2时,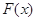 ≥0,即
≥0,即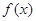 ≤
≤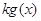 恒成立,
恒成立,
(3)若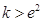 ,则
,则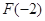 =
=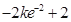 =
=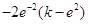 <0,
∴当
<0,
∴当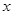 ≥-2时,
≥-2时,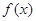 ≤
≤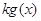 不可能恒成立,
不可能恒成立,
综上所述,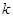 的取值范围为[1,
的取值范围为[1,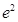 ].
].
考点:1.导数的几何意义;2.利用导数求函数单调区间;3.利用导数求函数最值.

练习册系列答案
相关题目
 -2lnx、
-2lnx、 -2lnx、
-2lnx、 -2lnx、
-2lnx、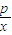 -2lnx、
-2lnx、