题目内容
5.设函数f(x)=x2-2x+3(x∈[t,t+1])的最小值为g(t),求g(t)的表达式.分析 先求出函数f(x)的对称轴x=1,从而可讨论区间[t,t+1]和对称轴的关系:分t+1≤1,t<1<t+1,和t≥1三种情况,然后根据二次函数在[t,t+1]上的单调性及取得顶点情况便可求出每种情况的f(x)的最小值,从而得出g(t)的表达式.
解答 解:f(x)的对称轴为x=1;
①t+1≤1,即t≤0时,f(x)在[t,t+1]上单调递减;
∴f(t+1)=t2+2是f(x)的最小值;
②t<1<t+1,即0<t<1时,f(1)=2是f(x)的最小值;
③t≥1时,f(x)在[t,t+1]上单调递增;
∴f(t)=t2-2t+3是f(x)的最小值;
∴综上得,$g(t)=\left\{\begin{array}{l}{{t}^{2}+2}&{t≤0}\\{2}&{0<t<1}\\{{t}^{2}-2t+3}&{t≥1}\end{array}\right.$.
点评 考查二次函数的对称轴,二次函数的单调性,以及根据单调性的定义求函数在闭区间上的最小值,以及根据抛物线顶点求二次函数最小值的方法.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.若定义域为R的奇函数f(x)=$\frac{x+n}{{{x^2}+m}}$在区间$(1,\frac{3}{2}]$上没有最小值,则实数m的取值范围是( )
| A. | (0,2] | B. | $[\frac{3}{2},2]$ | C. | $[\frac{3}{2},+∞)$ | D. | $(\frac{3}{2},+∞)$ |
16.过点(-2,3),倾斜角等于直线2x-y+3=0的倾斜角的直线方程为( )
| A. | -2x+y-7=0 | B. | -x+2y-8=0 | C. | 2x+y+1=0 | D. | x+2y-4=0 |
20.函数y=log2|x|的图象特点为( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
10.设Sn是等比数列{an}的前n项和,若$\frac{{{S_{504}}}}{{{S_{1008}}}}$=$\frac{1}{10}$,则$\frac{{{S_{1008}}}}{{{S_{2016}}}}$=( )
| A. | $\frac{1}{26}$ | B. | $\frac{1}{82}$ | C. | $\frac{2}{5}$ | D. | $\frac{10}{729}$ |
17.在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁.为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:
附表:
参照附表,下列结论正确的是( )
| 感染 | 未感染 | 总计 | |
| 服用 | 10 | 40 | 50 |
| 未服用 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.76 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗有关” | |
| B. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗无关” | |
| C. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗有关” | |
| D. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗无关” |
15.已知全集U=R,集合A={x|x+1<0},B={x|x2+3x<0},则 A∩B等于( )
| A. | {x|-3<x<0} | B. | {x|-3<x<-1} | C. | {x|x<-1} | D. | {x|-1≤x<0} |
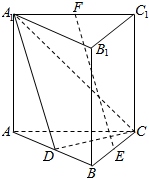 已知△ABC的三边长分别为AB=5,BC=4,AC=3,M是AB边上的点,P是平面ABC外一点,给出下列四个命题:
已知△ABC的三边长分别为AB=5,BC=4,AC=3,M是AB边上的点,P是平面ABC外一点,给出下列四个命题: