题目内容
19.若曲线$\frac{{x}^{2}}{4}$+$\frac{y|y|}{9}$=1和曲线kx+y-3=0有三个交点,则k的取值范围是(-$\frac{3\sqrt{2}}{2}$,-$\frac{3}{2}$)∪($\frac{3}{2}$,$\frac{3\sqrt{2}}{2}$).分析 由题意,y≥0,$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}$=1,y<0,$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{9}$=1,渐近线方程为y=±$\frac{3}{2}$,作出图象,即可得出结论.
解答  解:由题意,y≥0,$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}$=1,y<0,$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{9}$=1,渐近线方程为y=±$\frac{3}{2}$,
解:由题意,y≥0,$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{9}$=1,y<0,$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{9}$=1,渐近线方程为y=±$\frac{3}{2}$,
如图所示,曲线kx+y-3=0与$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{9}$=1联立,可得(9-4k2)x2+24kx-72=0,
∴△=(24k)2+288(9-4k2)=0,
∴k=±$\frac{3\sqrt{2}}{2}$,
结合图象,可得k的取值范围是(-$\frac{3\sqrt{2}}{2}$,-$\frac{3}{2}$)∪($\frac{3}{2}$,$\frac{3\sqrt{2}}{2}$),
故答案为:(-$\frac{3\sqrt{2}}{2}$,-$\frac{3}{2}$)∪($\frac{3}{2}$,$\frac{3\sqrt{2}}{2}$).
点评 本题考查曲线与方程,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.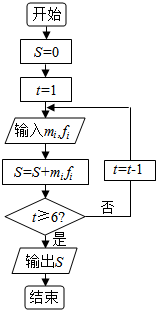 “世界睡眠日”定在每年的3月21日.2015年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站2015年3月13日到3月20日持续一周的在线调查,共有200人参加调查,现将数据整理分组如题中表格所示.为了对数据进行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图.
“世界睡眠日”定在每年的3月21日.2015年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站2015年3月13日到3月20日持续一周的在线调查,共有200人参加调查,现将数据整理分组如题中表格所示.为了对数据进行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图.
(1)求表格中m与n的值
(2)求输出S的值
(3)S的统计意义是什么?
 “世界睡眠日”定在每年的3月21日.2015年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站2015年3月13日到3月20日持续一周的在线调查,共有200人参加调查,现将数据整理分组如题中表格所示.为了对数据进行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图.
“世界睡眠日”定在每年的3月21日.2015年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站2015年3月13日到3月20日持续一周的在线调查,共有200人参加调查,现将数据整理分组如题中表格所示.为了对数据进行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图. | 序号 (i) | 分组 睡眠时间 | 组中值 (mi) | 频数 (人数) | 频率 (fi) |
| 1 | [4,5) | 4.5 | 8 | 0.04 |
| 2 | [5,6) | 5.5 | 52 | 0.26 |
| 3 | [6,7) | 6.5 | m | 0.30 |
| 4 | [7,8) | 7.5 | 56 | 0.28 |
| 5 | [8,9) | 8.5 | 20 | n |
| 6 | [9,10] | 9.5 | 4 | 0.02 |
(2)求输出S的值
(3)S的统计意义是什么?
11.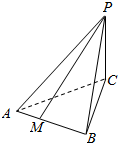 已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )
已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )
 已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )
已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )| A. | 2$\sqrt{43}$ | B. | $\sqrt{43}$ | C. | $\sqrt{11}$ | D. | 2$\sqrt{11}$ |