题目内容
已知k∈R,且k≠0,是否存在虚数z同时满足:①|z-1|=1;②k•z2+z+1=0.若存在,请求出复数z;若不存在,请说明理由.
分析:对于存在性问题,可先假设存在,即假设存在虚数z=a+bi(a,b∈R,且b≠0)同时满足两个条件,再利用复数的模及复数的乘法运算,求出z=a+bi中的a,b,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:不存在,---------------------------------------------------------(2分)
假设存在虚数z=a+bi(a,b∈R,且b≠0)同时满足两个条件,-----(4分)
由条件①|z-1|=1得a2+b2-2a=0,------(1)------------------(6分)
由条件②k•z2+z+1=0得
,----------------(9分)
∵k≠0,b≠0,∴a≠0,得a2+b2+2a=0---(2)------------(12分)
由(1)(2)式得a=b=0与b≠0矛盾,---------------------------(13分)
∴不存在虚数z同时满足①②两个条件-------------------------------(15分)
假设存在虚数z=a+bi(a,b∈R,且b≠0)同时满足两个条件,-----(4分)
由条件①|z-1|=1得a2+b2-2a=0,------(1)------------------(6分)
由条件②k•z2+z+1=0得
|
∵k≠0,b≠0,∴a≠0,得a2+b2+2a=0---(2)------------(12分)
由(1)(2)式得a=b=0与b≠0矛盾,---------------------------(13分)
∴不存在虚数z同时满足①②两个条件-------------------------------(15分)
点评:复数方程的化简,以及复数的模的运算,注意存在性问题的处理方法,是中档题.

练习册系列答案
相关题目
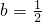 ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.