题目内容
已知a∈R，且α≠kπ+
，k∈Z设直线l：y=xtanα+m，其中m≠0，给出下列结论：
①l的倾斜角为arctan（tanα）；
②l的方向向量与向量
=(cosα，sinα)共线；
③l与直线xsinα-ycosα+n=0（n≠m）一定平行；
④若0＜a＜
，则l与y=x直线的夹角为
-α；
⑤若α≠kπ+
，k∈Z，与l关于直线y=x对称的直线l'与l互相垂直．
其中真命题的编号是
| π |
| 2 |
①l的倾斜角为arctan（tanα）；
②l的方向向量与向量
| a |
③l与直线xsinα-ycosα+n=0（n≠m）一定平行；
④若0＜a＜
| π |
| 4 |
| π |
| 4 |
⑤若α≠kπ+
| π |
| 4 |
其中真命题的编号是
②④
②④
（写出所有真命题的编号）分析：①当直线l的倾斜角为锐角时，倾斜角才为arctan（tanα）；②写出直线的方向向量即可的答案；③要注意区分向量的平行与直线平行；④由直线倾斜角的定义，结合图象可得；⑤可举反例说明．
解答：解：①当直线l的倾斜角为锐角时，倾斜角为arctan（tanα），当为钝角时应为π-arctan（tanα），故错误；
②直线l的方向向量为
=（1，tanα），显然有1×sinα-cosα•tanα=0，即两向量共线，故正确；
③由②得知识可知两直线的方向向量共线，但直线有可能平行或重合，故错误；
④由直线倾斜角的定义可知：直线y=x与x轴的正方向的夹角为
，又0＜a＜
，则l与y=x直线的夹角为
-α，故正确；
⑤若α≠kπ+
，k∈Z，与l关于直线y=x对称的直线l'与l不一定互相垂直，比如α=
，则l′的倾斜角为
，显然不垂直，故错误．
故答案为：②④
②直线l的方向向量为
| b |
③由②得知识可知两直线的方向向量共线，但直线有可能平行或重合，故错误；
④由直线倾斜角的定义可知：直线y=x与x轴的正方向的夹角为
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
⑤若α≠kπ+
| π |
| 4 |
| π |
| 6 |
| π |
| 3 |
故答案为：②④
点评：本题为直线的倾斜角和直线与直线的位置关系的问题，涉及直线的方向向量，属基础题．
练习册系列答案
相关题目
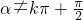，k∈Z设直线l：y=xtanα+m，其中m≠0，给出下列结论：
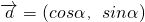共线；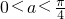
，则l与y=x直线的夹角为
；
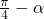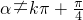，k∈Z，与l关于直线y=x对称的直线l'与l互相垂直．