题目内容
已知k∈R,a>0且a≠1,b>0且b≠1,函数f(x)=ax+k•bx.
(1)如果实数a、b满足a>1,ab=1,试判断函数f(x)的奇偶性,并说明理由;
(2)设a>1>b>0,k≤0,判断函数f(x)在R上的单调性并加以证明;
(3)若a=2,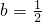 ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
解:(1)由已知,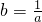 ,于是f(x)=ax+k•a-x,则f(-x)=a-x+k•ax,…(1分)
,于是f(x)=ax+k•a-x,则f(-x)=a-x+k•ax,…(1分)
若f(x)是偶函数,则f(x)=f(-x),即ax+k•a-x=a-x+k•ax,
所以(k-1)(ax-a-x)=0对任意实数x恒成立,所以k=1.…(3分)
若f(x)是奇函数,则f(-x)=-f(x),即a-x+k•ax=-(ax+k•a-x),
所以(k+1)(ax+a-x)=0对任意实数x恒成立,所以k=-1.…(5分)
综上,当k=1时,f(x)是偶函数;
当k=-1时,f(x)奇函数,
当k≠±1,f(x)既不是奇函数也不是偶函数.…(6分)
(2)因为a>1,0<b<1,所以函数y=ax是增函数,y=bx减函数,
由k≤0知,y=ax+k•bx是增函数,所以函数f(x)在R是增函数.…(8分)
证明如下:
设x1、x2∈R且x1<x2,
则 =
=
因为a>1,0<b<1,x1<x2,k≤0,
所以 ,
, ,
,
所以f(x2)-f(x1)>0,
所以函数f(x)在R是增函数.…(11分)
(3)f(x)=2x+k•2-x,若函数f(x)的图象是轴对称图形,
且对称轴是直线x=m,则函数f(x+m)是偶函数,
即对任意实数x,f(m-x)=f(m+x),…(14分)
2m-x+k•2-(m-x)=2m+x+k•2-(m+x),
化简得(2x-2-x)(2m-k•2-m)=0,…(16分)
因为上式对任意x∈R成立,
所以2m-k•2-m=0, .…(17分)
.…(17分)
所以,函数f(x)的图象是轴对称图形,其对称轴是直线 .…(18分)
.…(18分)
分析:(1)根据已知条件,将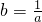 代入函数表达式,得f(x)=ax+k•a-x,再利用奇函数和偶函数的定义,用比较系数的方法,得出函数奇偶性的两种不同情况;
代入函数表达式,得f(x)=ax+k•a-x,再利用奇函数和偶函数的定义,用比较系数的方法,得出函数奇偶性的两种不同情况;
(2)因为a>1,0<b<1,根据指数函数单调性的定理,可得函数y=ax是增函数,y=bx减函数,再根据函数单调性的运算法则,得出函数f(x)=ax+k•bxR上的是增函数,最后用函数单调性的定义加以证明;
(3)根据函数f(x)=2x+k•2-x的图象是轴对称图形且对称轴是直线x=m,则函数f(x+m)是偶函数,即得到即对任意实数x,f(m-x)=f(m+x),代入表达式,采用比较系数法,可得2m-k•2-m=0,最终求出 .
.
点评:本题是一道函数综合题,属于难题.着重考查了函数的单调性与奇偶性和函数图象的对称性,解题时要注意有关定义和结论的正确理解与准确应用.
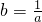 ,于是f(x)=ax+k•a-x,则f(-x)=a-x+k•ax,…(1分)
,于是f(x)=ax+k•a-x,则f(-x)=a-x+k•ax,…(1分)若f(x)是偶函数,则f(x)=f(-x),即ax+k•a-x=a-x+k•ax,
所以(k-1)(ax-a-x)=0对任意实数x恒成立,所以k=1.…(3分)
若f(x)是奇函数,则f(-x)=-f(x),即a-x+k•ax=-(ax+k•a-x),
所以(k+1)(ax+a-x)=0对任意实数x恒成立,所以k=-1.…(5分)
综上,当k=1时,f(x)是偶函数;
当k=-1时,f(x)奇函数,
当k≠±1,f(x)既不是奇函数也不是偶函数.…(6分)
(2)因为a>1,0<b<1,所以函数y=ax是增函数,y=bx减函数,
由k≤0知,y=ax+k•bx是增函数,所以函数f(x)在R是增函数.…(8分)
证明如下:
设x1、x2∈R且x1<x2,
则
 =
=
因为a>1,0<b<1,x1<x2,k≤0,
所以
 ,
, ,
,所以f(x2)-f(x1)>0,
所以函数f(x)在R是增函数.…(11分)
(3)f(x)=2x+k•2-x,若函数f(x)的图象是轴对称图形,
且对称轴是直线x=m,则函数f(x+m)是偶函数,
即对任意实数x,f(m-x)=f(m+x),…(14分)
2m-x+k•2-(m-x)=2m+x+k•2-(m+x),
化简得(2x-2-x)(2m-k•2-m)=0,…(16分)
因为上式对任意x∈R成立,
所以2m-k•2-m=0,
 .…(17分)
.…(17分)所以,函数f(x)的图象是轴对称图形,其对称轴是直线
 .…(18分)
.…(18分)分析:(1)根据已知条件,将
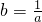 代入函数表达式,得f(x)=ax+k•a-x,再利用奇函数和偶函数的定义,用比较系数的方法,得出函数奇偶性的两种不同情况;
代入函数表达式,得f(x)=ax+k•a-x,再利用奇函数和偶函数的定义,用比较系数的方法,得出函数奇偶性的两种不同情况;(2)因为a>1,0<b<1,根据指数函数单调性的定理,可得函数y=ax是增函数,y=bx减函数,再根据函数单调性的运算法则,得出函数f(x)=ax+k•bxR上的是增函数,最后用函数单调性的定义加以证明;
(3)根据函数f(x)=2x+k•2-x的图象是轴对称图形且对称轴是直线x=m,则函数f(x+m)是偶函数,即得到即对任意实数x,f(m-x)=f(m+x),代入表达式,采用比较系数法,可得2m-k•2-m=0,最终求出
 .
.点评:本题是一道函数综合题,属于难题.着重考查了函数的单调性与奇偶性和函数图象的对称性,解题时要注意有关定义和结论的正确理解与准确应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.