题目内容
 如图所示,扇形AOB,圆心角AOB的大小等于
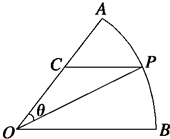
如图所示,扇形AOB,圆心角AOB的大小等于 ,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
,半径为2,在半径OA上有一动点C,过点C作平行于OB的直线交弧AB于点P.
(1)若C是半径OA的中点,求线段PC的大小;
(2)设∠COP=θ,求△POC面积的最大值及此时θ的值.
 解:(1)在△POC中,
解:(1)在△POC中,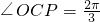 ,OP=2,OC=1,
,OP=2,OC=1,由
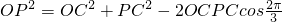
得PC2+PC-3=0,解得
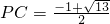 .
.(2)解法一:∵CP∥OB,∴
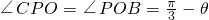 ,
,在△POC中,由正弦定理得
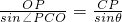 ,
,即
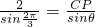 ,∴
,∴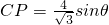 .
.又
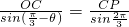 ,∴
,∴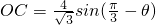 .
.记△POC的面积为S(θ),则
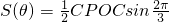 =
=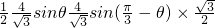
=
 =
=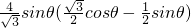 =
=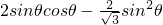
=
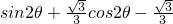 =
=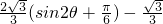 ,
,∴
 时,S(θ)取得最大值为
时,S(θ)取得最大值为 .
.解法二:
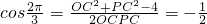 ,即OC2+PC2+OC•PC=4.
,即OC2+PC2+OC•PC=4.又OC2+PC2+OC•PC≥3OC•PC,即3OC•PC≤4,当且仅当OC=PC时等号成立,
所以
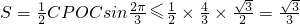 ,∵OC=PC,
,∵OC=PC,∴
 时,S(θ)取得最大值为
时,S(θ)取得最大值为 .
.分析:(1)在△POC中,根据
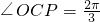 ,OP=2,OC=1,利用余弦定理求得PC的值.
,OP=2,OC=1,利用余弦定理求得PC的值.(2)解法一:利用正弦定理求得CP和OC的值,记△POC的面积为S(θ),则
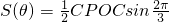 ,利用
,利用两角和差的正弦公式化为
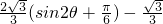 ,可得
,可得 时,S(θ)取得最大值为
时,S(θ)取得最大值为 .
.解法二:利用余弦定理求得OC2+PC2+OC•PC=4,再利用基本不等式求得3OC•PC≤4,所以
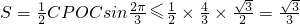 ,再根据OC=PC 求得△POC面积的最大值时θ的值.
,再根据OC=PC 求得△POC面积的最大值时θ的值.点评:本题主要考查两角和差的正弦公式,正弦定理、余弦定理、基本不等式的,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
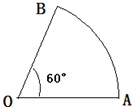 如图所示,扇形AOB中,
如图所示,扇形AOB中,
 (2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于
(2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于 (2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于
(2013•宝山区二模)如图所示,扇形AOB,圆心角AOB的大小等于
