题目内容
已知函数f(x)是R上的偶函数,且在(0,+∞)上是增函数,若f(-1)=0,那xf(x)<0的解集是
- A.(-1,0)∪(1,+∞)
- B.(-∞,-1)∪(0,1)
- C.(-∞,-1)∪(1,+∞)
- D.(-1,0)∪(0,1)
B
分析:确定函数在(-∞,0)上是减函数,f(1)=0,关于x的不等式xf(x)<0等价于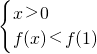 或
或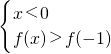 ,由此可得结论.
,由此可得结论.
解答:∵函数f(x)是R上的偶函数,且在(0,+∞)上是增函数,
∴函数在(0,+∞)上是增函数,在(-∞,0)上是减函数,
又f(-1)=0,故f(1)=0,
关于x的不等式xf(x)<0等价于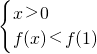 或
或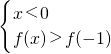
∴0<x<1或x<-1
∴xf(x)<0的解集是(-∞,-1)∪(0,1)
故选B.
点评:本题考查函数单调性与奇偶性的结合,考查解不等式,属于中档题.
分析:确定函数在(-∞,0)上是减函数,f(1)=0,关于x的不等式xf(x)<0等价于
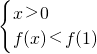 或
或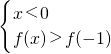 ,由此可得结论.
,由此可得结论.解答:∵函数f(x)是R上的偶函数,且在(0,+∞)上是增函数,
∴函数在(0,+∞)上是增函数,在(-∞,0)上是减函数,
又f(-1)=0,故f(1)=0,
关于x的不等式xf(x)<0等价于
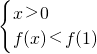 或
或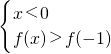
∴0<x<1或x<-1
∴xf(x)<0的解集是(-∞,-1)∪(0,1)
故选B.
点评:本题考查函数单调性与奇偶性的结合,考查解不等式,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目