Question

【题目】点为轴正半轴上一点， 两点关于轴对称，过点任作直线交抛物线于两点.（Ⅰ）求证： ；

（Ⅱ）若点的坐标为，且,试求所有满足条件的直线的解析式.

Answer 1

【答案】（1）见解析；（2）.

【解析】试题分析：（1）利用抛物线的图象上点的坐标特征，待定系数法球函数解析式，根与系数的关系和相似三角形的判定与性质解答即可；
（2）利用（1）中已知与结论，继续由相似三角形，根与系数的关系、函数解析式求得结果．

试题解析：

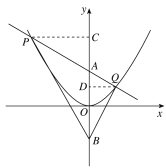
解：（1）如图，分别过点作为轴的垂线，垂足分别为.设点的坐标为，则点的坐标为.设直线的函数解析式为，并设的坐标分别为.由得，于是，即.

于是.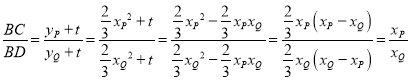

又因为，所以.

因为，所以∽，故.

（2）设，不妨设，由（1）可知

，所以.

因为,所以∽.于是,即，

所以,由（1）中，即，所以，

于是可求得.将代入，得到点的坐标（）.

再将点的坐标代入，求得.所以解析式为.