题目内容
如图，正方形上连接等腰直角三角形，直角三角形边上再连接正方形，…，无限重复，设正方形的面积S1，S2，S3，…，三角形的面积为T1，T2，T3，…，当S1的边长为2时，这些正方形和三角形的面积总和为（ ）
A．10
B．11
C．12
D．13
【答案】分析：正方形的边长构成以2为首项，以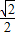
为公比的等比数列，等腰直角三角形的腰长也构成以
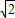为首项，
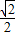为公比的等比数列，它们的面积，也构成等比数列，求这两个面积数列的各项和即可得答案．
解答：解：依题意，正方形的面积S1，S2，S3，…，构成以4为首项，以
为公比的等比数列，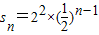
其各项和s=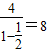
三角形的面积为T1，T2，T3，…，构成以1为首项，以
为公比的等比数列，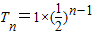
，其各项和t=
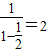，所以面积的各项和为s+t=10
故选 A
点评：本题考查无穷递缩等比数列的各项和应用，解题时要认真审题，仔细解答，避免错误
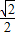为公比的等比数列，等腰直角三角形的腰长也构成以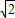为首项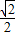，为公比的等比数列，它们的面积，也构成等比数列，求这两个面积数列的各项和即可得答案．解答：解：依题意，正方形的面积S1，S2，S3，…，构成以4为首项，以
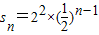为公比的等比数列，其各项和s=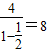三角形的面积为T1，T2，T3，…，构成以1为首项，以
为公比的等比数列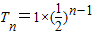，，其各项和t=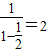，所以面积的各项和为s+t=10故选 A
点评：本题考查无穷递缩等比数列的各项和应用，解题时要认真审题，仔细解答，避免错误
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
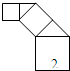如图，正方形上连接等腰直角三角形，直角三角形边上再连接正方形，…，无限重复，设正方形的面积S1，S2，S3，…，三角形的面积为T1，T2，T3，…，当S1的边长为2时，这些正方形和三角形的面积总和为（ ）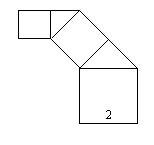
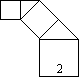
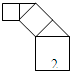如图，正方形上连接等腰直角三角形，直角三角形边上再连接正方形，…，无限重复，设正方形的面积S1，S2，S3，…，三角形的面积为T1，T2，T3，…，当S1的边长为2时，这些正方形和三角形的面积总和为