题目内容
△ABC中,角A,B,C所对的边分别为a,b,c,且满足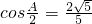 ,
,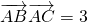 .
.
(1)求sinA的值;
(2)求△ABC的面积.
解:(1)因为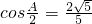 ,
,
∴cosA=2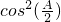 -1=
-1= ,sinA=
,sinA= -------------------------(6分)
-------------------------(6分)
(2) •
• =|
=| |•|
|•| |×cosA=3,得|
|×cosA=3,得| |•|
|•| |=5..
|=5..
故S△ABC= |
| |×|
|×| |×sinA=2--------------------------------------(12分)
|×sinA=2--------------------------------------(12分)
分析:(1)△ABC中,由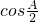 =
= 可求得cosA=
可求得cosA= ,从而可求得sinA的值;
,从而可求得sinA的值;
(2)由 •
• =|
=| |•|
|•| |×cosA=3,可求得|
|×cosA=3,可求得| |•|
|•| |=5,从而可求得△ABC的面积.
|=5,从而可求得△ABC的面积.
点评:本题考查平面向量数量积的运算,考查正弦定理中面积公式的应用,考查三角函数中的倍角公式的应用,属于中档题.
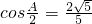 ,
,∴cosA=2
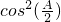 -1=
-1= ,sinA=
,sinA= -------------------------(6分)
-------------------------(6分)(2)
 •
• =|
=| |•|
|•| |×cosA=3,得|
|×cosA=3,得| |•|
|•| |=5..
|=5..故S△ABC=
 |
| |×|
|×| |×sinA=2--------------------------------------(12分)
|×sinA=2--------------------------------------(12分)分析:(1)△ABC中,由
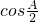 =
= 可求得cosA=
可求得cosA= ,从而可求得sinA的值;
,从而可求得sinA的值;(2)由
 •
• =|
=| |•|
|•| |×cosA=3,可求得|
|×cosA=3,可求得| |•|
|•| |=5,从而可求得△ABC的面积.
|=5,从而可求得△ABC的面积.点评:本题考查平面向量数量积的运算,考查正弦定理中面积公式的应用,考查三角函数中的倍角公式的应用,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目