题目内容
集合A={(x,y)|y=-x2+mx-1},B={(x,y)|y=3-x,0≤x≤3}.
(1)当m=4时,求A∩B;
(2)若A∩B是只有一个元素的集合,求实数m的取值范围.
(1)当m=4时,求A∩B;
(2)若A∩B是只有一个元素的集合,求实数m的取值范围.
分析:(1)将m=4代入A确定出A,联立A与B中欧的函数解析式,求出交点坐标,即为两集合的交集;
(2)集合A表示抛物线上的点,抛物线y=-x2+mx-1,开口向下且过点(0,-1),集合B表示线段上的点,要使A∩B只有一个元素,则线段与抛物线的位置关系有以下两种,分别求出m的范围即可.
(2)集合A表示抛物线上的点,抛物线y=-x2+mx-1,开口向下且过点(0,-1),集合B表示线段上的点,要使A∩B只有一个元素,则线段与抛物线的位置关系有以下两种,分别求出m的范围即可.
解答:解:(1)当m=4时,集合A={(x,y)|y=-x2+4x-1},B={(x,y)|y=3-x,0≤x≤3},
联立得:
,
消去y得:3-x=-x2+4x-1,
即(x-1)(x-4)=0,
解得:x=1或x=4(不合题意,舍去),
将x=1代入y=3-x得y=2,
则A∩B={(1,2)};
(2)集合A表示抛物线上的点,抛物线y=-x2+mx-1,开口向下且过点(0,-1),集合B表示线段上的点,
要使A∩B只有一个元素,则线段与抛物线的位置关系有以下两种,如图:
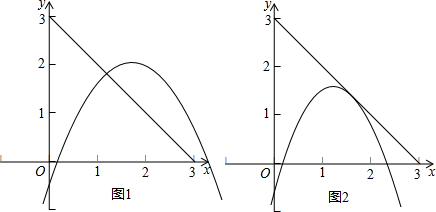
(i)由图1知,在函数f(x)=-x2+mx-1中,只要f(3)≥0,即-9+3m-1≥0,
解得:m≥
;
(ii)由图2知,抛物线与直线在x∈[0,3]上相切,
联立得:
,
消去y得:-x2+mx-1=3-x,
整理得:x2-(m+1)x+4=0,
当△=(m+1)2-16=0,
∴m=3或m=-5,
当m=3时,切点(2,1)适合,当m=-5时,切点(-2,5)舍去,
综上,m范围为m=3或m≥
.
联立得:
|
消去y得:3-x=-x2+4x-1,
即(x-1)(x-4)=0,
解得:x=1或x=4(不合题意,舍去),
将x=1代入y=3-x得y=2,
则A∩B={(1,2)};
(2)集合A表示抛物线上的点,抛物线y=-x2+mx-1,开口向下且过点(0,-1),集合B表示线段上的点,
要使A∩B只有一个元素,则线段与抛物线的位置关系有以下两种,如图:

(i)由图1知,在函数f(x)=-x2+mx-1中,只要f(3)≥0,即-9+3m-1≥0,
解得:m≥
| 10 |
| 3 |
(ii)由图2知,抛物线与直线在x∈[0,3]上相切,
联立得:
|
消去y得:-x2+mx-1=3-x,
整理得:x2-(m+1)x+4=0,
当△=(m+1)2-16=0,
∴m=3或m=-5,
当m=3时,切点(2,1)适合,当m=-5时,切点(-2,5)舍去,
综上,m范围为m=3或m≥
| 10 |
| 3 |
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
设集合A=B={(x,y)|x∈R,y∈R},从A到B的映射f:(x,y)→(x+2y,2x-y),则在映射f下B中的元素(1,1)对应的A中元素为( )
| A、(1,3) | ||||
| B、(1,1) | ||||
C、(
| ||||
D、(
|