题目内容
（本小题满分12分）已知函数f(x)=lg(x2 + a x + 1)的定义域为R ，在此条件下，解关于x的不等式 x2-2x + a(2-a)＜ 0 .
解：由f(x)=lg(x2 + a x + 1)的定义域为R得：△=a2-4＜0, ……………2分
解得：-2＜a＜2 ………………………… 4分
原不等式可化为：（x-a）[x - (2-a)]＜ 0 ………………………… 5分
(1) 当-2＜a＜1时，解得：a＜x＜2-a ；
(2) 当a=1时，不等式化为 （x-1）2 ＜0, 此时无解；
(3) 当1＜a＜2时，解得：2-a＜x＜a ； …………
…………… 10分
综上所述：当-2＜a＜1时，解集为：{ x ︱a＜x＜2-a };
当a=1时, 解集为：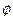
当1＜a＜2时，解集为：{ x ︱2-a＜x＜a } ………………… 12分
解析
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
