题目内容
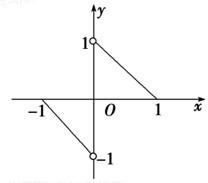 函数f(x)的图象是两条直线的一部分(如图所示),其定义域为[-1,0)∪(0,1],则不等式f(x)-f(-x)>-1的解集是( )
函数f(x)的图象是两条直线的一部分(如图所示),其定义域为[-1,0)∪(0,1],则不等式f(x)-f(-x)>-1的解集是( )| A、{x|-1≤x≤1且x≠0} | ||
| B、{x|-1≤x<0} | ||
C、{x|-1≤x<0或
| ||
D、{x|-1≤x<-
|
分析:由图可知,f(x)为奇函数.由有f(-x)=-f(x)将f(x)-f(-x)>-1转化,再用图象求解.
解答: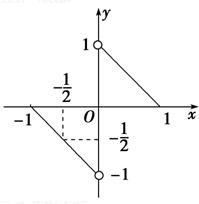 解:由图可知,f(x)为奇函数.
解:由图可知,f(x)为奇函数.
∴f(-x)=-f(x),
∴f(x)-f(-x)>-1
可转化为:2f(x)>-1
转化为f(x)>-
如图解得:-1≤x<-
或0<x≤1.
故选D.
 解:由图可知,f(x)为奇函数.
解:由图可知,f(x)为奇函数.∴f(-x)=-f(x),
∴f(x)-f(-x)>-1
可转化为:2f(x)>-1
转化为f(x)>-
| 1 |
| 2 |
如图解得:-1≤x<-
| 1 |
| 2 |
故选D.
点评:本题通过函数图象来考查函数的奇偶性,图象的分布及不等式问题,还考查了学生读图用图的基本能力.

练习册系列答案
相关题目
如图,函数f(x)的图象是曲线OAB,则f(
)的值等于( )
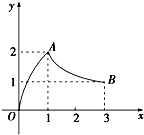
| 1 |
| f(3) |

| A、1 | B、2 | C、3 | D、0 |