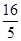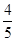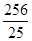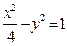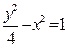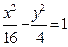题目内容
已知椭圆C: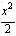 + y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若
+ y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若 = 3
= 3 ,则|
,则|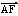 |等于
|等于
A.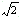 | B.2 | C.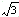 | D.3 |
A
解析考点:向量在几何中的应用.
专题:计算题;综合题.
解答:解:由条件,∵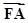 =3
=3
∴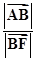 =
=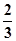
B点到直线L的距离设为BE,则 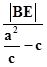 =
=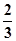
∴|BE|=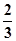
根据椭圆定义e=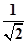 =
= 从而求出|BF|=
从而求出|BF|=
∴| |=
|= ×3=
×3=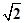
故答案为A.
点评:此题是中档题.本题主要考查了椭圆的应用.解题中灵活利用了椭圆的第二定义,是解题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
与双曲线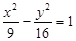 有共同的渐近线,且经过点
有共同的渐近线,且经过点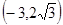 的双曲线的方程为
的双曲线的方程为
A.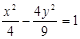 | B.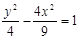 | C. | D.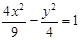 |
设点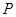 是双曲线
是双曲线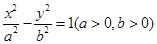 与圆
与圆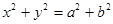 在第一象限的交点,其中
在第一象限的交点,其中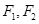 分别是双曲线的左、右焦点,且
分别是双曲线的左、右焦点,且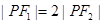 ,则双曲线的离心率为
,则双曲线的离心率为
A.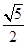 | B.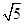 | C.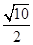 | D. |
已知圆的方程x2+y2=4,若抛物线过点A(0,-1),B(0,1)且以圆的切线为准线,则抛物线的焦点轨迹方程是( )
| A.+=1(y≠0) | B.+=1(y≠0) |
| C.+=1(x≠0) | D.+=1(x≠0) |
.设双曲线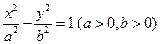 的渐近线与抛物线
的渐近线与抛物线 相切,则该双曲线的离心率为 ( )
相切,则该双曲线的离心率为 ( )
| A.3 | B. | C.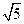 | D. |
双曲线 的离心率
的离心率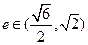 ,则m的取值范围是
,则m的取值范围是
A.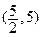 | B.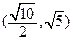  | C.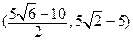 | D.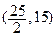 |
已知双曲线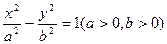 的实轴长、虚轴长、焦距长成等差数列,
的实轴长、虚轴长、焦距长成等差数列,
则此双曲线的离心率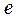 为( )
为( )
| A. | B. | C.2 | D.3 |
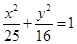 的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( )
的左右焦点为F1,F2,点P-在椭圆上,若P,F1,F2是一个直角三角形的三个顶点,则点P到x轴的距离是 ( )