题目内容
已知圆的方程x2+y2=4,若抛物线过点A(0,-1),B(0,1)且以圆的切线为准线,则抛物线的焦点轨迹方程是( )
| A.+=1(y≠0) | B.+=1(y≠0) |
| C.+=1(x≠0) | D.+=1(x≠0) |
解析

练习册系列答案
相关题目
已知椭圆C: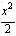 + y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若
+ y2=1的右焦点为F,右准线为l,点A∈l,线段AF交C于点B,若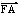 = 3
= 3 ,则|
,则|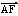 |等于
|等于
A.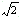 | B.2 | C.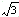 | D.3 |
设抛物线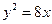 的焦点为F,准线为
的焦点为F,准线为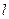 ,P为抛物线上一点,PA⊥
,P为抛物线上一点,PA⊥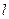 ,A为垂足.如果直线AF的斜率为
,A为垂足.如果直线AF的斜率为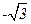 ,那么|PF|=………………………………………………………………………………………… ( )
,那么|PF|=………………………………………………………………………………………… ( )
| A.8 | B.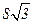 | C.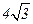 | D.4 |
.已知实数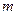 是
是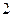 ,
,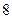 的等比中项,则双曲线
的等比中项,则双曲线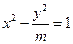 的离心率为( )
的离心率为( )
A.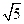 | B.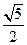 | C.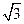 | D. |
抛物线 的焦点到准线的距离为( )
的焦点到准线的距离为( )
| A.1 | B.2 | C.4 | D.8 |
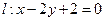 过椭圆左焦点F1和一个顶点B,则该椭圆的离心率为 ( )
过椭圆左焦点F1和一个顶点B,则该椭圆的离心率为 ( )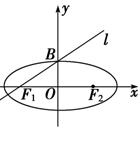
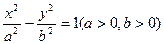 的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该双曲线左支的两个交点,且
的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该双曲线左支的两个交点,且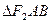 是等边三角形,则双曲线的离心率为 ( )
是等边三角形,则双曲线的离心率为 ( )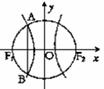
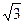
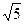
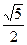
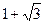
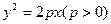 焦点为F,准线为l,经过F的直线与抛物线交于A、B两点,交准线于C点,点A在x轴上方,AK⊥l,垂足为K,若|BC|=2|BF|,且|AF|=4,则△AKF的面积是 ( )
焦点为F,准线为l,经过F的直线与抛物线交于A、B两点,交准线于C点,点A在x轴上方,AK⊥l,垂足为K,若|BC|=2|BF|,且|AF|=4,则△AKF的面积是 ( )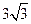 C.
C.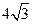 D.8
D.8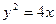 的焦点为
的焦点为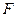 ,准线与
,准线与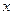 轴的交点为
轴的交点为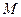 ,
,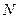 为抛物线上的一点,且
为抛物线上的一点,且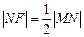 ,则
,则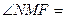 ( )
( )