题目内容
已知数列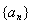 的前n项和为Sn,对一切正整数n,点
的前n项和为Sn,对一切正整数n,点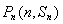 在函数
在函数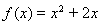 的图像上,且过点
的图像上,且过点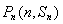 的切线的斜率为kn.
的切线的斜率为kn.
(1)求数列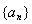 的通项公式;
的通项公式;
(2)若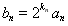 ,求数列
,求数列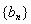 的前n项和Tn.
的前n项和Tn.
【答案】
(1)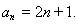 (2)
(2)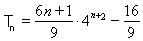 .
.
【解析】
试题分析:(1)根据点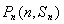 都在函数
都在函数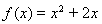 的图像上,得到
的图像上,得到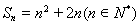 .利用“两步一验”即得数列的通项公式.
.利用“两步一验”即得数列的通项公式.
(2)由导数的几何意义得到 ,
,
从而可利用“错位相减法”求数列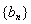 的前n项和Tn
的前n项和Tn
本题综合性较强,但解题思路明确,难度适中.
试题解析:(1) 点
点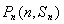 都在函数
都在函数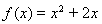 的图像上,
的图像上,

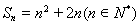 . 2分
. 2分
当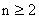 时,
时,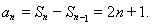
当 时,
时, 满足上式,
满足上式,
所以数列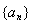 的通项公式为
的通项公式为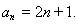 6分
6分
(2)由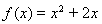 求导可得
求导可得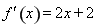 ,
,
因为过点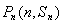 的切线的斜率为
的切线的斜率为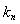 ,
, ,
,
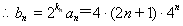 ,
,


两式相减得
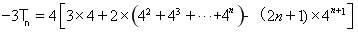 9分
9分
 . 12分
. 12分
考点:导数的几何意义,数列的通项公式,“错位相减法”.

练习册系列答案
相关题目
 求使不等式
求使不等式 的前n项和为
的前n项和为 ,
, 且满足
且满足 +n (n>1且n∈
+n (n>1且n∈ )
) ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值  的前n项和为
的前n项和为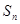 ,且
,且 ,
, ,并猜想
,并猜想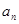 的表达式。
的表达式。